题目内容
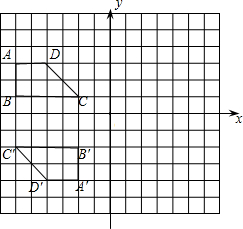 在直角坐标系中,两个全等的梯形ABCD和A′B′C′D′的位置如图所示,图中小正方形的边长为1个长度单位.
在直角坐标系中,两个全等的梯形ABCD和A′B′C′D′的位置如图所示,图中小正方形的边长为1个长度单位.(1)把梯形ABCD绕点C顺时针方向旋转90°,画出相应的图形A1B1C1D1;
(2)把梯形ABCD向右平移8个单位得梯形A2B2C2D2,梯形A2B2C2D2是否可看成由梯形A′B′C′D′经过轴对称变换或中心对称变换得到?若是,请写出对称轴的解析式或对称中心坐标;若不是,请说明理由.
分析:(1)根据旋转角度、旋转中心及旋转方向可得出各点的对应点,顺次连接即可得出答案.
(2)画出梯形A2B2C2D2即可作出判断.
(2)画出梯形A2B2C2D2即可作出判断.
解答:解:(1)所画图形如下:
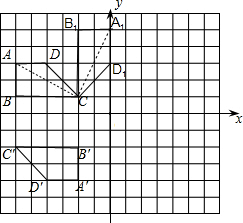 ;
;
(2)
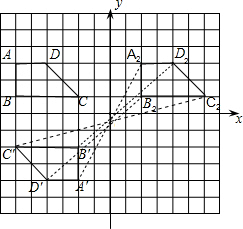
∴梯形A2B2C2D2可看成由四边形A′B′C′D′经过中心变换得到,对称中心坐标(0,-
).
 ;
;(2)

∴梯形A2B2C2D2可看成由四边形A′B′C′D′经过中心变换得到,对称中心坐标(0,-
| 1 |
| 2 |
点评:本题考查平移作图、旋转作图及中心对称的性质,综合了几种变换,有一定的难度,在(3)问中要将对应点连线,看是否满足中心对称.

练习册系列答案
相关题目
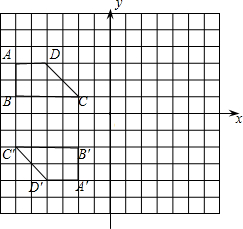 在直角坐标系中,两个全等的梯形ABCD和A′B′C′D′的位置如图所示,图中小正方形的边长为1个长度单位.
在直角坐标系中,两个全等的梯形ABCD和A′B′C′D′的位置如图所示,图中小正方形的边长为1个长度单位.