题目内容
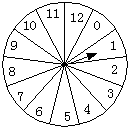如图，对于给定的转盘，指针停于各个数字部分的概率都相等．小兰和小青两人做游戏，如果指针停在偶数，则小兰赢．如果指针停在3的倍数，则小青赢，那么这个游戏对小兰和小青公平吗？谁获胜的概率大？若不公平，你能修改游戏规则，使之公平吗？
分析：根据概率公式，即可求得小兰与小青获胜的概率，比较概率：概率相等就公平，否则就不公平．使之公平的游戏规则只要满足小兰与小青获胜的概率相等即可．
解答：答：不公平．
小兰获胜的概率是
，小青获胜的概率是
，
所以小兰获胜的概率大．
修改游戏规则，如：如果指针停在偶数，则小兰赢．如果指针停在奇数，则小青赢，这样对两人都公平．
小兰获胜的概率是
| 1 |
| 2 |
| 1 |
| 3 |
所以小兰获胜的概率大．
修改游戏规则，如：如果指针停在偶数，则小兰赢．如果指针停在奇数，则小青赢，这样对两人都公平．
点评：本题考查的是游戏公平性的判断．判断游戏公平性就要计算每个事件的概率，概率相等就公平，否则就不公平．
练习册系列答案
孟建平名校考卷系列答案
相关题目
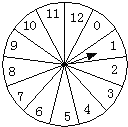若对于给定的转盘，如图所示的指针停于各个数字部分的概率都相等．假设该指针不会停在两个不同部分的分界线上．则该指针停在奇数部分的概率为（ ）A、
| ||
B、
| ||
C、
| ||
D、
|
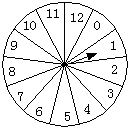如图，对于给定的转盘，指针停于各个数字部分的概率都相等．小兰和小青两人做游戏，如果指针停在偶数，则小兰赢．如果指针停在3的倍数，则小青赢，那么这个游戏对小兰和小青公平吗？谁获胜的概率大？若不公平，你能修改游戏规则，使之公平吗？
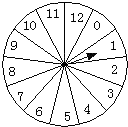若对于给定的转盘，如图所示的指针停于各个数字部分的概率都相等．假设该指针不会停在两个不同部分的分界线上．则该指针停在奇数部分的概率为
