题目内容
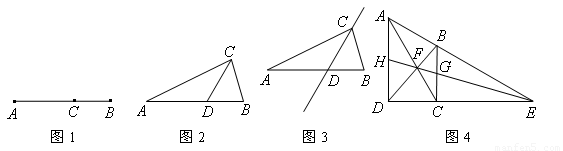
 如图,梯形上、下底分别为a,b,高线长恰好等于圆的直径2r,则图中阴影部分的面积是
如图,梯形上、下底分别为a,b,高线长恰好等于圆的直径2r,则图中阴影部分的面积是
- A.(a+b)r-πr2
- B.abr-πr2
- C.2(a+b)r-πr2
- D.2abr-πr2
A
分析:本题的等量关系为:图中阴影部分的面积=梯形面积-圆的面积.根据等量关系直接求出结果.
解答:依题意得,
 ×(a+b)×2r-π×(
×(a+b)×2r-π×(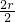 )2=(a+b)r-πr2.
)2=(a+b)r-πr2.
故选A.
点评:解决问题的关键是读懂题意,找到所求的量的等量关系.需注意梯形面积、圆的面积公式的运用.
分析:本题的等量关系为:图中阴影部分的面积=梯形面积-圆的面积.根据等量关系直接求出结果.
解答:依题意得,
 ×(a+b)×2r-π×(
×(a+b)×2r-π×(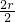 )2=(a+b)r-πr2.
)2=(a+b)r-πr2.故选A.
点评:解决问题的关键是读懂题意,找到所求的量的等量关系.需注意梯形面积、圆的面积公式的运用.

练习册系列答案
相关题目
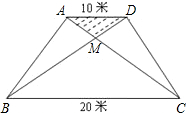 带种满花后,已经花了500元,请你预算一下,若继续在△BMC地带种植同样的太阳花,资金是否够用?并说明理由.
带种满花后,已经花了500元,请你预算一下,若继续在△BMC地带种植同样的太阳花,资金是否够用?并说明理由.

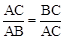 ,那么称点C为线段AB的黄金分割点。某数学兴趣小组在进行课题研究时,由黄金分割点联想到“黄金分割线”,类似地给出“黄金分割线”的定义:直线l将一个面积为S的图形分成两部分,这两部分的面积分别为S1、S2,如果
,那么称点C为线段AB的黄金分割点。某数学兴趣小组在进行课题研究时,由黄金分割点联想到“黄金分割线”,类似地给出“黄金分割线”的定义:直线l将一个面积为S的图形分成两部分,这两部分的面积分别为S1、S2,如果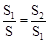 ,那么称直线l为该图形的黄金分割线.
,那么称直线l为该图形的黄金分割线.
 ,那么称点C为线段AB的黄金分割点。某数学兴趣小组在进行课题研究时,由黄金分割点联想到“黄金分割线”,类似地给出“黄金分割线”的定义:直线l将一个面积为S的图形分成两部分,这两部分的面积分别为S1、S2,如果
,那么称点C为线段AB的黄金分割点。某数学兴趣小组在进行课题研究时,由黄金分割点联想到“黄金分割线”,类似地给出“黄金分割线”的定义:直线l将一个面积为S的图形分成两部分,这两部分的面积分别为S1、S2,如果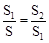 ,那么称直线l为该图形的黄金分割线.
,那么称直线l为该图形的黄金分割线.