题目内容
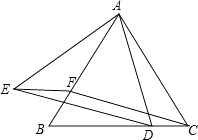
【题目】如图,△ABC为等边三角形,D、F分别为BC、AB上的点,且CD=BF. 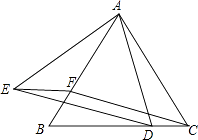
(1)求证:△ACD≌△CBF;
(2)以AD为边作等边三角形△ADE,点D在线段BC上的何处时,四边形CDEF是平行四边形.
【答案】
(1)证明:∵△ABC为等边三角形,
∴∠B=∠ACD=60°,AC=BC,
在△ACD和△CBF中
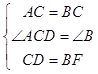 ,
,
∴△ACD≌△CBF(SAS);
(2)解:D点在任意位置,四边形CDFE是平行四边形,
∵∠BDE+60=∠DAC+60,
∴∠BDE=∠DAC,
又∵∠DAC=∠BCF,
∴∠BDE=∠BCF,
∴ED∥CF,
又∵△ACD≌△CBF,
∴CF=AD=DE,
∴四边形是CDEF平行四边形.
【解析】(1)直接利用等边三角形的性质结合全等三角形的判定与性质得出答案;(2)直接利用等边三角形的性质结合平行四边形的判定方法得出答案.
【考点精析】本题主要考查了等边三角形的性质和平行四边形的判定的相关知识点,需要掌握等边三角形的三个角都相等并且每个角都是60°;两组对边分别平行的四边形是平行四边形:两组对边分别相等的四边形是平行四边形;一组对边平行且相等的四边形是平行四边形;两组对角分别相等的四边形是平行四边形;对角线互相平分的四边形是平行四边形才能正确解答此题.

练习册系列答案
相关题目
【题目】某商场一名业务员12个月的销售额(单位:万元)如下表:
月份(月) | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
销售额(万元) | 6.2 | 9.8 | 9.8 | 7.8 | 7.2 | 6.4 | 9.8 | 7.8 | 7 | 9.8 | 10 | 7.5 |
则这组数据的众数和中位数分别是( )
A.10,8B.9.8,7.8C.9.8,7.9D.9.8,8.1