题目内容
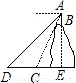
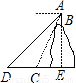
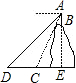 如图,在一座山的山顶B处用高为1米的测倾器望地面C、D两点,测得的俯角分别为60°和45°,若已知DC的长是20米,求山高BE.(结果可用根式表示)
如图,在一座山的山顶B处用高为1米的测倾器望地面C、D两点,测得的俯角分别为60°和45°,若已知DC的长是20米,求山高BE.(结果可用根式表示)
分析:欲求BE的长,需先求出AE的长;可分别在Rt△ADE和Rt△ACE中,用AE表示出DE、CE的长,根据DC=DE-CE=20,即可求得AE的值,由此得解.
解答:解:在Rt△ACE中,有CE=AE•tan30°,
在Rt△ADE中,有DE=AE•tan45°,
∴DC=DE-CE=AE(tan45°-tan30°),
∴AE=
=30+10
,
∴BE=AE-AB=(29+10
)米.
答:山的高度为(29+10
)米.
在Rt△ADE中,有DE=AE•tan45°,
∴DC=DE-CE=AE(tan45°-tan30°),
∴AE=
| 20 |
| tan45°-tan30° |
| 3 |
∴BE=AE-AB=(29+10
| 3 |
答:山的高度为(29+10
| 3 |
点评:本题考查直角三角形的解法,应利用俯角构造直角三角形,再借助角边关系、三角函数的定义解题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
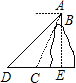 如图,在一座山的山顶B处用高为1米的测倾器望地面C、D两点,测得的俯角分别为60°和45°,若已知DC的长是20米,求山高BE.(结果可用根式表示)
如图,在一座山的山顶B处用高为1米的测倾器望地面C、D两点,测得的俯角分别为60°和45°,若已知DC的长是20米,求山高BE.(结果可用根式表示)