题目内容
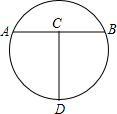 如图,线段CD所在的直线垂直平分线段AB,且AB=CD=8cm,将这样的工具放在一个圆中,使A、B、D三点落在圆上,则此圆形工件的半径是( )
如图,线段CD所在的直线垂直平分线段AB,且AB=CD=8cm,将这样的工具放在一个圆中,使A、B、D三点落在圆上,则此圆形工件的半径是( )分析:根据线段CD垂直平分线段AB,得出AC=
AB,AC2+OC2=AO2,再设⊙O的半径为r,求出42+(8-r)2=r2,然后解方程即可.
| 1 |
| 2 |
解答: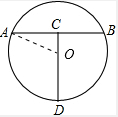 解:∵线段CD垂直平分线段AB,
解:∵线段CD垂直平分线段AB,
∴A、B、D三点所在圆的圆心O在CD上,
AC=
AB=
×8=4cm,
∵AC2+OC2=AO2,
连接AO,
设⊙O的半径为r,
∵CD=8cm,
∴OC=(8-r)cm,
∴42+(8-r)2=r2,
解得:r=5cm;
故选C.
 解:∵线段CD垂直平分线段AB,
解:∵线段CD垂直平分线段AB,∴A、B、D三点所在圆的圆心O在CD上,
AC=
| 1 |
| 2 |
| 1 |
| 2 |
∵AC2+OC2=AO2,
连接AO,
设⊙O的半径为r,
∵CD=8cm,
∴OC=(8-r)cm,
∴42+(8-r)2=r2,
解得:r=5cm;
故选C.
点评:此题考查了垂径定理的应用,关键是找出圆心,通过作辅助线构造直角三角形,用到的知识点是垂径定理、勾股定理、解一元二次方程.

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
 如图,在平面直角坐标系中,A、B均在边长为1的正方形网格格点上.
如图,在平面直角坐标系中,A、B均在边长为1的正方形网格格点上.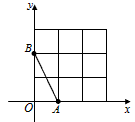
 、
、 均在边长为1的正方形网格格点上.
均在边长为1的正方形网格格点上.
 沿x轴向右平移2格得线段CD,请你求出线段CD所在的直线函数解析式.
沿x轴向右平移2格得线段CD,请你求出线段CD所在的直线函数解析式.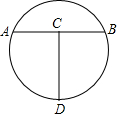 如图,线段CD所在的直线垂直平分线段AB,且AB=CD=8cm,将这样的工具放在一个圆中,使A、B、D三点落在圆上,则此圆形工件的半径是
如图,线段CD所在的直线垂直平分线段AB,且AB=CD=8cm,将这样的工具放在一个圆中,使A、B、D三点落在圆上,则此圆形工件的半径是