题目内容
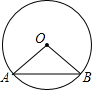 (2008•宝安区二模)如图,AB是直径为10cm的⊙O的一条弦,若AB=5
(2008•宝安区二模)如图,AB是直径为10cm的⊙O的一条弦,若AB=5| 3 |
分析:过圆心O作OD⊥AB于点D.由垂径定理求得AD=BD=
AB;然后在直角三角形OAD中利用勾股定理即可求得OD的长度;最后根据三角形的面积公式来求△OAB的面积.
| 1 |
| 2 |
解答: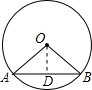 解:过圆心O作OD⊥AB于点D,则AD=BD=
解:过圆心O作OD⊥AB于点D,则AD=BD=
AB=
.
在Rt△OAD中,OA=5cm,AD=
,
由勾股定理知,OD=
=
,
则△OAB的面积为:
AB•OD=
×5
cm×
cm=
cm2.
故选C.
 解:过圆心O作OD⊥AB于点D,则AD=BD=
解:过圆心O作OD⊥AB于点D,则AD=BD=| 1 |
| 2 |
5
| ||
| 2 |
在Rt△OAD中,OA=5cm,AD=
5
| ||
| 2 |
由勾股定理知,OD=
| OA2-AD2 |
| 5 |
| 2 |
则△OAB的面积为:
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 5 |
| 2 |
25
| ||
| 4 |
故选C.
点评:本题考查了垂径定理、勾股定理.此类在圆中涉及弦长、半径的计算的问题,常把半弦长,圆心到弦距离转换到同一直角三角形中,然后通过直角三角形予以求解,常见辅助线是过圆心作弦的垂线.

练习册系列答案
相关题目
 (2008•宝安区二模)如图,实心圆台的左视图是( )
(2008•宝安区二模)如图,实心圆台的左视图是( ) (2008•宝安区二模)如图,按照流程输入的数据进入第一个舱后,运算结果全部进入第二个舱,经过第二次运算后全部输出的数据是( )
(2008•宝安区二模)如图,按照流程输入的数据进入第一个舱后,运算结果全部进入第二个舱,经过第二次运算后全部输出的数据是( )