题目内容
(2004•湖州)(注意:本题为自选题,供考生选做.自选题得分将记入本学科的总分,但考生所得总分最多为120分.)二次函数y=ax2+bx+c图象的一部分如图所示,则a的取值范围是______.
【答案】分析:由抛物线的开口方向判断a的符号,由抛物线与y轴的交点得出c的值,然后根据图象经过的点的情况进行推理,进而推出所得结论.
解答:解:抛物线开口向下,a<0,
图象过点(0,1),c=1,
图象过点(1,0),a+b+c=0,
∴b=-(a+c)=-(a+1).
由题意知,当x=-1时,应有y>0,
∴a-b+c>0,
∴a+(a+1)+1>0,
∴a>-1,
∴实数a的取值范围是-1<a<0.
点评:根据开口判断a的符号,根据与x轴,y轴的交点判断c的值以及b用a表示出的代数式.难点是推断出当x=-1时,应有y>0.
解答:解:抛物线开口向下,a<0,
图象过点(0,1),c=1,
图象过点(1,0),a+b+c=0,
∴b=-(a+c)=-(a+1).
由题意知,当x=-1时,应有y>0,
∴a-b+c>0,
∴a+(a+1)+1>0,
∴a>-1,
∴实数a的取值范围是-1<a<0.
点评:根据开口判断a的符号,根据与x轴,y轴的交点判断c的值以及b用a表示出的代数式.难点是推断出当x=-1时,应有y>0.

练习册系列答案
 口算能手系列答案
口算能手系列答案
相关题目

 经过点A(2,-3),则k的值是 .
经过点A(2,-3),则k的值是 . 经过点A(2,-3),则k的值是 .
经过点A(2,-3),则k的值是 .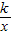 经过点A(2,-3),则k的值是 .
经过点A(2,-3),则k的值是 .