题目内容
附加题:已知二次函数y=ax2+bx+c的图象G和x轴有且只有一个交点A,与y轴的交点为B(0,4),且ac=b.(1)求该二次函数的解析表达式;
(2)将一次函数y=-3x的图象作适当平移,使它经过点A,记所得的图象为L,图象L与G的另一个交点为C,求△ABC的面积.
【答案】分析:(1)根据二次函数与x轴只有一个交点,可得出△=0,然后将B点坐标代入抛物线,联立△=0和ac=b即可求出抛物线的解析式.
(2)根据抛物线的解析式可求出A点的坐标,设出平移后的直线的解析式,然后将A点坐标代入即可求出平移后图象L的解析式,然后联立直线L和抛物线G即可求出C点的坐标.由于△ABC的面积无法直接求出,可转换成其他规则图形面积的和差来求解.
过C作x轴的垂线,可通过S△ABC=S梯形OBCD-S△CAD-S△OBA来求出△ABC的面积.
解答: 解:(1)由B(0,4)得,c=4.
解:(1)由B(0,4)得,c=4.
G与x轴的交点A( ,0),
,0),
由条件ac=b,得 =
= ,
,
即A(-2,0).
所以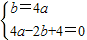 .
.
解得 .
.
所求二次函数的解析式为y=x2+4x+4.
(2)设图象L的函数解析式为y=-3x+b,
因图象L过点A(-2,0),
所以b=-6,
即平移后所得一次函数的解析式为
y=-3x-6.
令-3x-6=x2+4x+4,
解得x1=-2,x2=-5.
将它们分别代入y=-3x-6,
得y1=0,y2=9.
所以图象L与G的另一个交点为C(-5,9).
如图,过C作CD⊥x轴于D,
则S△ABC=S梯形BCDO-S△ACD-S△ABO
= (4+9)×5-
(4+9)×5- ×3×9-
×3×9- ×2×4=15.
×2×4=15.
点评:命题立意:考查二次函数解析式的确定、图形的面积求法、函数图象交点等知识及综合应用知识、解决问题的能力.
点评:(1)函数图象交点坐标为两函数解析式组成的方程组的解.
(2)不规则图形的面积通常转化为规则图形的面积的和差.
(2)根据抛物线的解析式可求出A点的坐标,设出平移后的直线的解析式,然后将A点坐标代入即可求出平移后图象L的解析式,然后联立直线L和抛物线G即可求出C点的坐标.由于△ABC的面积无法直接求出,可转换成其他规则图形面积的和差来求解.
过C作x轴的垂线,可通过S△ABC=S梯形OBCD-S△CAD-S△OBA来求出△ABC的面积.
解答:
 解:(1)由B(0,4)得,c=4.
解:(1)由B(0,4)得,c=4.G与x轴的交点A(
 ,0),
,0),由条件ac=b,得
 =
= ,
,即A(-2,0).
所以
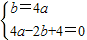 .
.解得
 .
.所求二次函数的解析式为y=x2+4x+4.
(2)设图象L的函数解析式为y=-3x+b,
因图象L过点A(-2,0),
所以b=-6,
即平移后所得一次函数的解析式为
y=-3x-6.
令-3x-6=x2+4x+4,
解得x1=-2,x2=-5.
将它们分别代入y=-3x-6,
得y1=0,y2=9.
所以图象L与G的另一个交点为C(-5,9).
如图,过C作CD⊥x轴于D,
则S△ABC=S梯形BCDO-S△ACD-S△ABO
=
 (4+9)×5-
(4+9)×5- ×3×9-
×3×9- ×2×4=15.
×2×4=15.点评:命题立意:考查二次函数解析式的确定、图形的面积求法、函数图象交点等知识及综合应用知识、解决问题的能力.
点评:(1)函数图象交点坐标为两函数解析式组成的方程组的解.
(2)不规则图形的面积通常转化为规则图形的面积的和差.

练习册系列答案
相关题目