题目内容
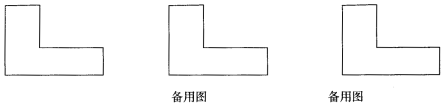
【题目】猜想与证明:如图①摆放矩形纸片ABCD与矩形纸片ECGF,使B,C,G三点在一条直线上,CE在边CD上.连结AF,若M为AF的中点,连结DM,ME,试猜想DM与ME的数量关系,并证明你的结论.
拓展与延伸:
(1)若将“猜想与证明”中的纸片换成正方形纸片ABCD与正方形纸片ECGF,其他条件不变,则DM和ME的关系为__________________;
(2)如图②摆放正方形纸片ABCD与正方形纸片ECGF,使点F在边CD上,点M仍为AF的中点,试证明(1)中的结论仍然成立.[提示:直角三角形斜边上的中线等于斜边的一半]
 ①
①  ②
②
【答案】猜想与证明:猜想DM与ME的数量关系是:DM=ME,证明见解析;拓展与延伸:(1)DM=ME,DM⊥ME;(2)证明见解析
【解析】
猜想:延长EM交AD于点H,利用△FME≌△AMH,得出HM=EM,再利用直角三角形中,斜边的中线等于斜边的一半证明.
(1)延长EM交AD于点H,利用△FME≌△AMH,得出HM=EM,再利用直角三角形中,斜边的中线等于斜边的一半证明,
(2)连接AC,AC和EC在同一条直线上,再利用直角三角形中,斜边的中线等于斜边的一半证明,
解:猜想与证明:
猜想DM与ME的数量关系是:DM=ME.
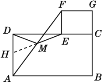
证明:如图①,延长EM交AD于点H.
 ①
①
∵四边形ABCD、四边形ECGF都是矩形,
∴AD∥BG,EF∥BG,∠HDE=90°.
∴AD∥EF.
∴∠AHM=∠FEM.
又∵AM=FM,∠AMH=∠FME,
∴△AMH≌△FME.
∴HM=EM.
又∵∠HDE=90°,
∴DM=![]() EH=ME;
EH=ME;
(1)∵四边形ABCD和CEFG是正方形,
∴AD∥EF,
∴∠EFM=∠HAM,
又∵∠FME=∠AMH,FM=AM,
在△FME和△AMH中,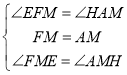 ,
,
∴△FME≌△AMH(ASA)
∴HM=EM,
在RT△HDE中,HM=EM,
∴DM=HM=ME,
∴DM=ME.
∵四边形ABCD和CEFG是正方形,
∴AD=CD,CE=EF,
∵△FME≌△AMH,
∴EF=AH,
∴DH=DE,
∴△DEH是等腰直角三角形,
又∵MH=ME,
故答案为:DM=ME,DM⊥ME;
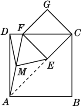
(2)证明:如图②,连结AC.
 ②
②
∵四边形ABCD、四边形ECGF都是正方形,
∴∠DCA=∠DCE=∠CFE=45°,
∴点E在AC上.
∴∠AEF=∠FEC=90°.
又∵点M是AF的中点,
∴ME=![]() AF.
AF.
∵∠ADC=90°,点M是AF的中点,
∴DM=![]() AF.
AF.
∴DM=ME.
∵ME=![]() AF=FM,DM=
AF=FM,DM=![]() AF=FM,
AF=FM,
∴∠DFM=![]() (180°-∠DMF),∠MFE=
(180°-∠DMF),∠MFE=![]() (180°-∠FME),
(180°-∠FME),
∴∠DFM+∠MFE= ![]() (180°-∠DMF)+
(180°-∠DMF)+ ![]() (180°-∠FME)
(180°-∠FME)
=180°-![]() (∠DMF+∠FME)
(∠DMF+∠FME)
=180°-![]() ∠DME.
∠DME.
∵∠DFM+∠MFE=180°-∠CFE=180°-45°=135°,
∴180°-![]() ∠DME=135°.
∠DME=135°.
∴∠DME=90°.
∴DM⊥ME.