题目内容
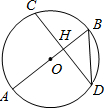如图，弦CD垂直于⊙O的直径AB，垂足为H，且CD=2| 2 |
| 3 |
| A、2 | B、3 | C、4 | D、5 |
分析：根据垂径定理和相交弦定理求解．
解答：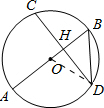
解：连接OD．
由垂径定理得HD=
，由勾股定理得HB=1，
设圆O的半径为R，在Rt△ODH中，
则R2=（
）2+（R-1）2，由此得2R=3，
或由相交弦定理得（
）2=1×（ 2R-1），由此得2R=3，所以AB=3
故选B．
解：连接OD．由垂径定理得HD=
| 2 |
设圆O的半径为R，在Rt△ODH中，
则R2=（
| 2 |
或由相交弦定理得（
| 2 |
故选B．
点评：本题主要考查：垂径定理、勾股定理或相交弦定理．
练习册系列答案
相关题目
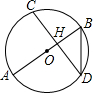如图，弦CD垂直于⊙O的直径AB，垂足为H，且CD=
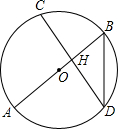如图，弦CD垂直于⊙O的直径AB，垂足为H，且CD=
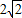，BD=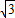
，则AB的长为 ．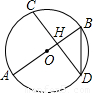
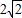，BD=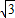
，则AB的长为（ ）