题目内容
 (2013•陕西)如图,四边形ABCD的对角线AC,BD相交于点O,且BD平分AC.若BD=8,AC=6,∠BOC=120°,则四边形ABCD的面积为
(2013•陕西)如图,四边形ABCD的对角线AC,BD相交于点O,且BD平分AC.若BD=8,AC=6,∠BOC=120°,则四边形ABCD的面积为12
| 3 |
12
.(结果保留根号)| 3 |
分析:如图,过点A作AE⊥BD于点E,过点C作CF⊥BD于点F.则通过解直角△AEO和直角△CFO求得AE=CF=
,所以易求四边形ABCD的面积.
3
| ||
| 2 |
解答: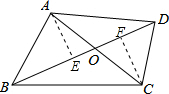 解:如图,过点A作AE⊥BD于点E,过点C作CF⊥BD于点F.
解:如图,过点A作AE⊥BD于点E,过点C作CF⊥BD于点F.
∵BD平分AC,AC=6,
∴AO=CO=3.
∵∠BOC=120°,
∴∠AOE=60°,
∴AE=AO•sin60°=
.
同理求得CF=
,
∴S四边形ABCD=S△ABD+S△CBD=
BD•AE+
BD•CF=2×
×
×8=12
.
故答案是:12
.
 解:如图,过点A作AE⊥BD于点E,过点C作CF⊥BD于点F.
解:如图,过点A作AE⊥BD于点E,过点C作CF⊥BD于点F.∵BD平分AC,AC=6,
∴AO=CO=3.
∵∠BOC=120°,
∴∠AOE=60°,
∴AE=AO•sin60°=
3
| ||
| 2 |
同理求得CF=
3
| ||
| 2 |
∴S四边形ABCD=S△ABD+S△CBD=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
3
| ||
| 2 |
| 3 |
故答案是:12
| 3 |
点评:本题考查了解直角三角形,三角形的面积的计算.求图中相关线段的长度时,也可以根据勾股定理进行解答.

练习册系列答案
相关题目
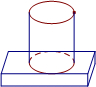 (2013•陕西)如图,下面的几何体是由一个圆柱和一个长方体组成的,则它的俯视图是( )
(2013•陕西)如图,下面的几何体是由一个圆柱和一个长方体组成的,则它的俯视图是( ) (2013•陕西)如图,AB∥CD,∠CED=90°,∠AEC=35°,则∠D的大小为( )
(2013•陕西)如图,AB∥CD,∠CED=90°,∠AEC=35°,则∠D的大小为( )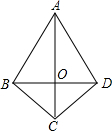 (2013•陕西)如图,在四边形ABCD中,AB=AD,CB=CD,若连接AC、BD相交于点O,则图中全等三角形共有( )
(2013•陕西)如图,在四边形ABCD中,AB=AD,CB=CD,若连接AC、BD相交于点O,则图中全等三角形共有( )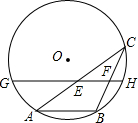 (2013•陕西)如图,AB是⊙O的一条弦,点C是⊙O上一动点,且∠ACB=30°,点E、F分别是AC、BC的中点,直线EF与⊙O交于G、H两点.若⊙O的半径为7,则GE+FH的最大值为
(2013•陕西)如图,AB是⊙O的一条弦,点C是⊙O上一动点,且∠ACB=30°,点E、F分别是AC、BC的中点,直线EF与⊙O交于G、H两点.若⊙O的半径为7,则GE+FH的最大值为