题目内容
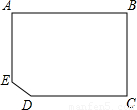
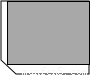
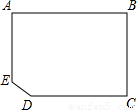
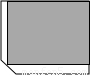
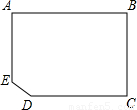
有一块缺角矩形地皮ABCDE（如图），其中AB=110m，BC=80m，CD=90m，∠EDC=135°，现准备用此块地建一座地基为长方形（图中用阴影部分表示）的教学大楼，以下四个方案中，地基面积最大的是（ ）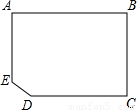
A．
B．
C．
D．
【答案】分析：本题利用矩形的性质，等腰直角三角形的性质以及函数的性质进行做题．
解答：
解：如图，作DG⊥AB于G，EF⊥BC于F，DG，EF交于O，设CN=x，
那么∠EDO=∠EDC-90°=45°，
因此△EOD是等腰直角三角形，同理△EQR，△RPD均为等腰直角三角形，
∴EO=OD=AB-CD=20，RP=DP=CN=x，EQ=QR=AM=EO-RP=20-x，AE=BC-OD=60，
如果设阴影部分MRNB的面积为y，
那么y=MR•RN=（AE+QR）•（CD+RP）=（80-x）（x+90）=7200-10x-x2
因为y是x的开口向下的抛物线，其对称轴为直线x=-5，
所以当x≥0时，二次函数为减函数，
所以此函数的最大值就是当x=0时，y=7200，
故选A．
点评：本题主要考查了矩形的性质，等腰直角三角形的性质以及函数的性质等知识点的应用，要注意多知识点的融会贯通．
解答：
解：如图，作DG⊥AB于G，EF⊥BC于F，DG，EF交于O，设CN=x，那么∠EDO=∠EDC-90°=45°，
因此△EOD是等腰直角三角形，同理△EQR，△RPD均为等腰直角三角形，
∴EO=OD=AB-CD=20，RP=DP=CN=x，EQ=QR=AM=EO-RP=20-x，AE=BC-OD=60，
如果设阴影部分MRNB的面积为y，
那么y=MR•RN=（AE+QR）•（CD+RP）=（80-x）（x+90）=7200-10x-x2
因为y是x的开口向下的抛物线，其对称轴为直线x=-5，
所以当x≥0时，二次函数为减函数，
所以此函数的最大值就是当x=0时，y=7200，
故选A．
点评：本题主要考查了矩形的性质，等腰直角三角形的性质以及函数的性质等知识点的应用，要注意多知识点的融会贯通．
练习册系列答案
相关题目
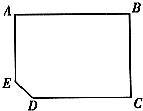5、有一块缺角矩形地皮ABCDE（如图），其中AB=110m，BC=80m，CD=90m，∠EDC=135°，现准备用此块地建一座地基为长方形（图中用阴影部分表示）的教学大楼，以下四个方案中，地基面积最大的是（ ）
