题目内容
阅读材料:如图(一),△ABC的周长为l,内切圆O的半径为r,连接OA、OB、OC,△ABC被划分为三个小三角形,用S△ABC表示△ABC的面积.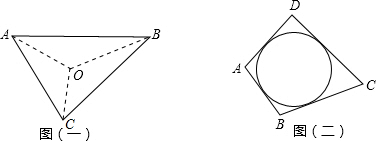
∵S△ABC=S△OAB+S△OBC+S△OCA
又∵S△OAB=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∴S△ABC=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
(1)理解与应用:利用公式计算边长分为5、12、13的三角形内切圆半径;
(2)类比与推理:若四边形ABCD存在内切圆(与各边都相切的圆,如图(二))且面积为S,各边长分别为a、b、c、d,试推导四边形的内切圆半径公式;
(3)拓展与延伸:若一个n边形(n为不小于3的整数)存在内切圆,且面积为S,各边长分别为a1、a2、a3、…、an,合理猜想其内切圆半径公式(不需说明理由).
分析:(1)根据上述三角形的内切圆的半径公式,由已知条件,结合勾股定理的逆定理得该三角形是直角三角形.可以首先求得其面积是30,其周长是5+12+13=30.再根据其公式代入计算;
(2)同样连接圆心和四边形的各个顶点以及圆心和的切点,根据四边形的面积等于四个直角三角形的面积进行计算;
(3)根据上述方法和结论,即可猜想到:任意多边形的内切圆的半径等于其面积的2倍除以多边形的周长.
(2)同样连接圆心和四边形的各个顶点以及圆心和的切点,根据四边形的面积等于四个直角三角形的面积进行计算;
(3)根据上述方法和结论,即可猜想到:任意多边形的内切圆的半径等于其面积的2倍除以多边形的周长.
解答:解:(1)以5,12,13为边长的三角形为直角三角形,易求得r=
=2;
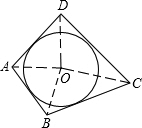
(2)连接OA,OB,OC,OD,并设内接圆半径为r,
可得S四边形ABCD=S△OAB+S△OBC+S△OCD+S△ODA
=
a•r+
b•r+
c•r+
d•r=
(a+b+c+d)•r.
∴r=
;
(3)猜想:r=
.
| 2×30 |
| 5+12+13 |

(2)连接OA,OB,OC,OD,并设内接圆半径为r,
可得S四边形ABCD=S△OAB+S△OBC+S△OCD+S△ODA
=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∴r=
| 2s |
| a+b+c+d |
(3)猜想:r=
| 2s |
| a1+a2+…+an |
点评:考查了学生由特殊推广到一般的能力,掌握多边形的内切圆的半径的计算方法.

练习册系列答案
相关题目
阅读材料:如图①,一扇窗户打开后用窗钩 可将其固定.
可将其固定.

(1)这里所运用的几何原理是( )
(2)如图②是图①中窗子开到一定位置时的平面图,若 ,
, ,
, =60cm,求点
=60cm,求点 到边
到边 的距离.(结果保留根号)
的距离.(结果保留根号)
 可将其固定.
可将其固定.
(1)这里所运用的几何原理是( )
| A.三角形的稳定性 | B.两点之间线段最短 |
| C.两点确定一条直线 | D.垂线段最短 |
 ,
, ,
, =60cm,求点
=60cm,求点 到边
到边 的距离.(结果保留根号)
的距离.(结果保留根号) 


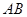 可将其固定.
可将其固定.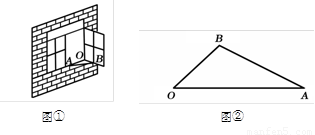
 ,
, ,
, =60cm,求点
=60cm,求点 到边
到边