题目内容
【题目】在平面直角坐标系中有点M(m,2m+3).
(1)若点M在x轴上,求m的值;
(2)若点M在第三象限内,求m的取值范围;
(3)点M在第二、四象限的角平分线上,求m的值.
【答案】
(1)解:∵M(m,2m+3)在x轴上,
∴2m+3=0,
∴m=﹣ ![]()
(2)解:∵M(m,2m+3)在第三象限内,
∴ ![]() ,
,
∴m<﹣ ![]()
(3)解:∵M(m,2m+3)在第二、四象限的角平分线上,
∴m+(2m+3)=0
∴m=﹣1.
【解析】(1)根据点在x轴上纵坐标为0,建立方程求解。
(2)根据点在第三象限横坐标,纵坐标都小于0,建立不等式组求解即可。
(3)根据第二、四象限的角平分线上的横坐标,纵坐标互为相反数,即横纵坐标之和=0,建立方程求解即可。
【考点精析】解答此题的关键在于理解解一元一次方程的步骤的相关知识,掌握先去分母再括号,移项变号要记牢.同类各项去合并,系数化“1”还没好.求得未知须检验,回代值等才算了,以及对一元一次不等式组的解法的理解,了解解法:①分别求出这个不等式组中各个不等式的解集;②利用数轴表示出各个不等式的解集;③找出公共部分;④用不等式表示出这个不等式组的解集.如果这些不等式的解集的没有公共部分,则这个不等式组无解 ( 此时也称这个不等式组的解集为空集 ).

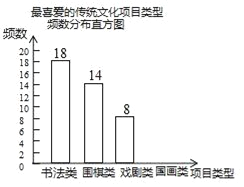
【题目】某校为更好地培养学生兴趣,开展“拓展课程走班选课”活动,随机抽查了部分学生,了解他们最喜爱的项目类型(分为书法、围棋、戏剧、国画共4类),并将统计结果绘制成如图不完整的频数分布表及频数分布直方图.
最喜爱的传统文化项目类型频数分布表
项目类型 | 频数 | 频率 |
书法类 | 18 | a |
围棋类 | 14 | 0.28 |
喜剧类 | 8 | 0.16 |
国画类 | b | 0.20 |
根据以上信息完成下列问题:
(1)频数分布表中a=_____,b=_____;
(2)补全频数分布直方图;
(3)若全校共有学生1500名,估计该校最喜爱围棋的学生大约有多少人?