题目内容
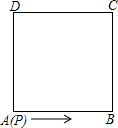（2013•大兴区一模）如图，正方形ABCD边长为2cm，动点P从A点出发，沿正方形的边按逆时针方向运动，当它的运动路程为2013cm时，线段PA的长为| 5 |
| 5 |
（8n-2）
（8n-2）
cm（用含n的代数式表示）．分析：先求出正方形的周长，再用2013除以8，根据余数的情况确定出点P的位置，然后利用勾股定理列式计算即可得解；
用正方形的n个周长减去AD的长度即可．
用正方形的n个周长减去AD的长度即可．
解答：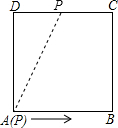
解：∵正方形ABCD边长为2cm，
∴周长为4×2=8cm，
2013÷8=251…5，
∴它的运动路程为2013cm时，点P在CD的中点处，
由勾股定理得，PA=
=
=
cm，
当点P第n次（n为正整数）到达点D时，点P的运动路程为8n-AD=（8n-2）cm．
故答案为：
；（8n-2）．
解：∵正方形ABCD边长为2cm，∴周长为4×2=8cm，
2013÷8=251…5，
∴它的运动路程为2013cm时，点P在CD的中点处，
由勾股定理得，PA=
| AD2+DP2 |
| 22+12 |
| 5 |
当点P第n次（n为正整数）到达点D时，点P的运动路程为8n-AD=（8n-2）cm．
故答案为：
| 5 |
点评：本题主要考查了正方形的性质，勾股定理的应用，比较简单，读懂题目信息，理解点P的运动变化规律是解题的关键．
练习册系列答案
暑假作业暑假快乐练西安出版社系列答案
相关题目
