题目内容
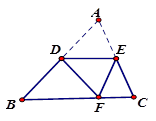
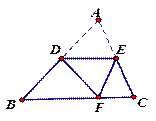
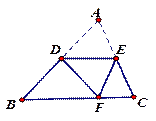
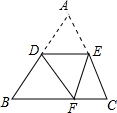如图，DE∥BC，将△ABC沿DE所在的直线折叠，点A正好落在BC边上F处，若∠B=40°，则∠BDF=________度．
100
分析：先根据图形翻折不变性的性质可得∠ADE=∠EDF，再由平行线的性质可得∠B=∠ADE=40°，最后由平角的性质即可求解．
解答：∵△DEF是△DEA沿直线DE翻折变换而来，
∴∠ADE=∠EDF，
∵DE∥BC，∠B=40°，
∴∠B=∠ADE=40°，
∴∠ADE=∠EDF=40°，
∴∠BDF=180°-∠ADE-∠EDF=180°-40°-40°=100°．
故答案为：100．
点评：本题考查的是图形翻折变换的性质及平行线的性质，熟知折叠的性质是解答此题的关键．
分析：先根据图形翻折不变性的性质可得∠ADE=∠EDF，再由平行线的性质可得∠B=∠ADE=40°，最后由平角的性质即可求解．
解答：∵△DEF是△DEA沿直线DE翻折变换而来，
∴∠ADE=∠EDF，
∵DE∥BC，∠B=40°，
∴∠B=∠ADE=40°，
∴∠ADE=∠EDF=40°，
∴∠BDF=180°-∠ADE-∠EDF=180°-40°-40°=100°．
故答案为：100．
点评：本题考查的是图形翻折变换的性质及平行线的性质，熟知折叠的性质是解答此题的关键．
练习册系列答案
阅读快车系列答案
相关题目
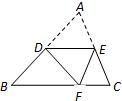12、如图，DE∥BC，将△ABC沿DE所在的直线折叠，点A正好落在BC边上F处，若∠B=40°，则∠BDF=
