题目内容
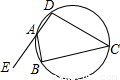
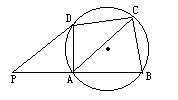
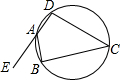如图，ABCD是圆内接四边形，E为DA延长线上的一点，若∠C=45°，AB=| 2 |
130°
130°
，点B到AE的距离为1
1
．分析：过B作BF⊥AE于F，则BF就是所求的距离；根据圆内接四边形的性质，易求出∠EAB=∠C=45°，即△ABF是等腰直角三角形，已知了斜边AB的长，即可求出直角边BF的长．
解答：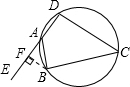
解：过点B作BF⊥AE于点F；
∵ABCD为圆内接四边形，若∠C=45°，
∴∠DAB+∠C=180°，∠EAB+∠BAD=180°，
∴∠BAD=135°．
∴∠EAB=∠C=45°
∴AF=BF
∵AB=
，
∴BF=1
∴点B到AE的距离为1．
解：过点B作BF⊥AE于点F；∵ABCD为圆内接四边形，若∠C=45°，
∴∠DAB+∠C=180°，∠EAB+∠BAD=180°，
∴∠BAD=135°．
∴∠EAB=∠C=45°
∴AF=BF
∵AB=
| 2 |
∴BF=1
∴点B到AE的距离为1．
点评：此题主要考查了圆的内接四边形的性质以及直角三角形的性质．
练习册系列答案
相关题目
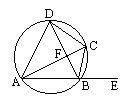
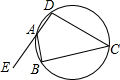如图，ABCD是圆内接四边形，E为DA延长线上的一点，若∠C=45°，AB=
，则∠BAD=________，点B到AE的距离为________．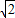
，则∠BAD= ，点B到AE的距离为 ．