Question

如图，正方形ABCD的边长为6，E是边BC上的一点，△ABE经过旋转后得到△ADF．

（1）旋转中心是点　    ；旋转角最少是　    度；
（2）求四边形AECF的面积；
（3）如果点G在边CD上，且GAE=45⁰，
①试判断GE、BE、DG之间有什么样的数量关系?并说明理由。
②若BE=2，求DG的长。

Answer 1

（1）旋转中心是点 A；最少旋转了 90°；
（2）36．
(3)①GE=BE+DG见解析
②DG的长为3.

试题分析：(1）△ABE按顺时针方向旋转后恰好与△ADF重合，AB与AD重合，这旋转角为∠BAD=90°，根据旋转的定义得到旋转中心是点 A；最少旋转了 90°；
（2）根据旋转的性质得△ABE≌△ADF，得△ABE≌△ADF，并且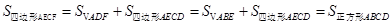，利用正方形的面积公式即可得到四边形BFDE的面积．
（3）①利用△ABE≌△ADF得出AE=AF，GAE=GAF,从而得出△AEG≌△AGF，证出EG=GF=GD+BE；
②设DG为x，然后利用勾股定理得出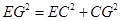，从而求出DG的长.
点评：本题考查了旋转的性质：旋转前后两图形全等，对应点到旋转中心的距离相等，对应点与旋转中心的连线段所夹的角等于旋转角．也考查了三角形全等的性质以及正方形的性质．