��Ŀ����
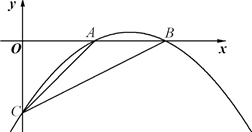 ��֪����ͼ��������y=ax2+bx-2��x����A��B���㣬��y���ڵ�C��OC=OA����ABC�����Ϊ2��
��֪����ͼ��������y=ax2+bx-2��x����A��B���㣬��y���ڵ�C��OC=OA����ABC�����Ϊ2����1���������ߵĽ���ʽ��
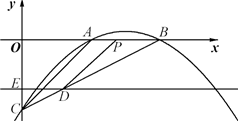
��2����ƽ����x��Ķ�ֱ��DE�ӵ�C��ʼ����ÿ��1����λ���ٶ���y��������ƽ�ƣ��ҷֱ�y�ᡢ�߶�BC�ڵ�E����D��ͬʱ����P�ӵ�B���������߶�OB����ÿ��2����λ���ٶ���ԭ��O�˶�������P�˶�����Oʱ��ֱ��DE���P��ֹͣ�˶�������DP�����P���˶�ʱ��Ϊt�룮
�ٵ�tΪ��ֵʱ��
| 1 |
| ED |
| 1 |
| OP |
���Ƿ����t��ֵ��ʹ��P��B��DΪ��������������ABC���ƣ������ڣ����t��ֵ���������ڣ���˵�����ɣ�
��������1�����C�����꣬�õ�A��B�����꣬�������ߵĽ���ʽΪy=a��x-2����x-4���������C���������a���ɣ�
��2���������⣺CE=t��PB=2t��OP=4-2t����ED��BA�ó�
=
�����ED=2CE=2t������
+
=
+
=
=
��������ɣ�����P��B��DΪ��������������ABC���������������
=
��
=
����������ɣ�
��2���������⣺CE=t��PB=2t��OP=4-2t����ED��BA�ó�
| ED |
| OB |
| CE |
| CO |
| 1 |
| ED |
| 1 |
| OP |
| 1 |
| 2t |
| 1 |
| 4-2t |
| 4 |
| 2t(4-2t) |
| 1 |
| -t2+2t |
| BP |
| AB |
| BD |
| BC |
| BP |
| BD |
| BC |
| BA |
����⣺��1����ͼ����������y=ax2+bx-2�ã�C��0��-2����
��OA=OC=2��
��A��2��0����
�ߡ�ABC�����Ϊ2��
��AB=2��
��B��4��0����
���������ߵĽ���ʽΪy=a��x-2����x-4���������C��0��-2����
a=-
��
�������ߵĽ���ʽΪy=-
(x-2)(x-4)=-
x2+
x-2��
�������ߵĽ���ʽΪy=-
x2+
x-2��
��2���⣺�����⣺CE=t��PB=2t��OP=4-2t��
��ED��BA
�ɵã�
=
��
��
=
��
��ED=2CE=2t��
��
+
=
+
=
=
��
�ߵ�t=1ʱ��-t2+2t�����ֵ1��
�൱t=1ʱ
+
��ֵ��С����СֵΪ1��
�𣺵�tΪ1ʱ��
+
��ֵ��С����Сֵ��1��
�ڽ⣺���������CD=
t��CB=2
��
��BD=2
-
t��
�ߡ�PBD=��ABC��
����P��B��D��������������ABC���������������
��
=
ʱ����
=
��
��ã�t=
��
��
=
ʱ����
=
��
��ã�t=
��
��t=
��t=
ʱ����P��B��DΪ��������������ABC���ƣ�
�𣺴���t��ֵ��ʹ��P��B��DΪ��������������ABC���ƣ�t��ֵ��
��
��
��OA=OC=2��
��A��2��0����
�ߡ�ABC�����Ϊ2��
��AB=2��
��B��4��0����
���������ߵĽ���ʽΪy=a��x-2����x-4���������C��0��-2����
a=-
| 1 |
| 4 |

�������ߵĽ���ʽΪy=-
| 1 |
| 4 |
| 1 |
| 4 |
| 3 |
| 2 |
�������ߵĽ���ʽΪy=-
| 1 |
| 4 |
| 3 |
| 2 |
��2���⣺�����⣺CE=t��PB=2t��OP=4-2t��
��ED��BA
�ɵã�
| ED |
| OB |
| CE |
| CO |
��
| ED |
| 4 |
| CE |
| 2 |
��ED=2CE=2t��
��
| 1 |
| ED |
| 1 |
| OP |
| 1 |
| 2t |
| 1 |
| 4-2t |
| 4 |
| 2t(4-2t) |
| 1 |
| -t2+2t |
�ߵ�t=1ʱ��-t2+2t�����ֵ1��
�൱t=1ʱ
| 1 |
| ED |
| 1 |
| OP |
�𣺵�tΪ1ʱ��
| 1 |
| ED |
| 1 |
| OP |
�ڽ⣺���������CD=
| 5 |
| 5 |
��BD=2
| 5 |
| 5 |
�ߡ�PBD=��ABC��
����P��B��D��������������ABC���������������
��
| BP |
| AB |
| BD |
| BC |
| 2t |
| 2 |
2
| ||||
2
|
��ã�t=
| 2 |
| 3 |
��
| BP |
| BD |
| BC |
| BA |
| 2t | ||||
2
|
2
| ||
| 2 |
��ã�t=
| 10 |
| 7 |
��t=
| 2 |
| 3 |
| 10 |
| 7 |
�𣺴���t��ֵ��ʹ��P��B��DΪ��������������ABC���ƣ�t��ֵ��
| 2 |
| 3 |
| 10 |
| 7 |
������������Ҫ����Զ��κ�������ֵ���ô���ϵ��������κ����Ľ���ʽ����һԪһ�η��̣����������ε����ʺ��ж����ۺ�������Щ���ʽ��м����ǽ����Ĺؼ���

��ϰ��ϵ�д�
�����Ŀ
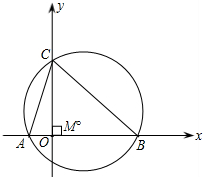 ��y�ύ��C��������Ϊ3����ABC�����Բ��Բ��Ϊ��M��
��y�ύ��C��������Ϊ3����ABC�����Բ��Բ��Ϊ��M�� ���������ϣ��������Ϊ12��
���������ϣ��������Ϊ12�� ��2013•�������ʼ죩��֪����ͼ��������y=ax2+bx+c��x�ύ�ڵ�A��
��2013•�������ʼ죩��֪����ͼ��������y=ax2+bx+c��x�ύ�ڵ�A�� ��֪����ͼ��������y=ax2-2ax+c��a��0����y�ύ�ڵ�C��0��4������x�ύ�ڵ�A��B����A������Ϊ��4��0����
��֪����ͼ��������y=ax2-2ax+c��a��0����y�ύ�ڵ�C��0��4������x�ύ�ڵ�A��B����A������Ϊ��4��0���� ��֪����ͼ��������y=x2+px+q��x���ཻ��A��B���㣬��y�ύ�ڵ�C����OA��OB��OA=OC���������ߵĶ���Ϊ��P��ֱ��PC��x��Ľ���Dǡ�����A����y��Գƣ�
��֪����ͼ��������y=x2+px+q��x���ཻ��A��B���㣬��y�ύ�ڵ�C����OA��OB��OA=OC���������ߵĶ���Ϊ��P��ֱ��PC��x��Ľ���Dǡ�����A����y��Գƣ�