题目内容
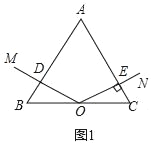
【题目】如图,∠MON=120°,△ABC是等边三角形,O点是边BC的中点,将△ABC绕点O逆时针旋转一定的角度,OM与边AB相交于点D,ON与边AC(或AC的延长线)相交于点E.
(1)如图1,若OD⊥AB,垂足为D,BC=4,求CE的长;
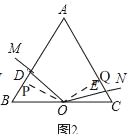
(2)如图2,当ON与AC边交于点E时,求证:BD+CE=![]() BC;
BC;
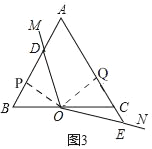
(3)如图3,当ON与AC边的延长线交于点E时,(2)中的结论还成立吗?如果成立,请证明;如果不成立,请直接写出线段BD、BC、CE之间的数量关系.

【答案】(1)1(2)见解析(3)不成立
【解析】【试题分析】(1)如图1,△ABC是等边三角形,根据等边三角形的性质得:∠B=∠C=60°,
因为点O是线段BC的中点,
根据中点的定义得:BO=OC=![]() BC=2.
BC=2.
因为OD⊥AB,得∠ODB=∠ODA=90°,
根据三角形内角和定理得:∠BOD=180°﹣60°﹣90°=30°,
在Rt△OBD中,BD=![]() OB=
OB=![]() ×2=1;
×2=1;
又∠OEA=360°﹣60°﹣90°﹣120°=90°,
即∠OEC=90°,
根据AAS得:△OBD≌△OCE,
根据全等三角形的性质得:CE=BD=1;
(2)转化为(1),利用相同的思路证明即可;
(3)(2)中的结论不成立,线段BD、BC、CE之间的数量关系为BD﹣CE=![]() BC.
BC.
理由: 由(1)知△OBP≌△OCQ,
根据全等三角形的性质得:BP=CQ,OP=OQ.
因为∠A=60°,利用四边形的内角和得:∠POQ=360°﹣60°﹣90°﹣90°=120°.
因为∠DOE=120°,利用等式的 性质得:∠POD=∠QOE.
根据ASA得:△POD≌△QOE,根据全等三角形的性质得:PD=EQ.在Rt△BOP中,∠B=60°,根据30°所对的直角边是斜边的一半得:BP=![]() OB=
OB=![]() BC
BC
得证:BD﹣CE=BP+PD﹣CE=CQ+EQ﹣CE=CQ+CQ+CE﹣CE=2CQ=2BP=2×![]() BC=
BC=![]() BC.
BC.
【试题解析】
(1)如图1,∵△ABC是等边三角形,
∴∠B=∠C=60°,
∵点O是线段BC的中点,
∴BO=OC=![]() BC=2.
BC=2.
∵OD⊥AB,得∠ODB=∠ODA=90°,
∴∠BOD=180°﹣60°﹣90°=30°,
在Rt△OBD中,BD=![]() OB=
OB=![]() ×2=1;
×2=1;
又∠OEA=360°﹣60°﹣90°﹣120°=90°,
∴∠OEC=90°,
∴△OBD≌△OCE,
∴CE=BD=1;

(2)过点O作OP⊥AB于P,作OQ⊥AC于Q,如图2,
则有∠OPD=∠OQE=90°.
同(1)的方法得,△OBP≌△OCQ,
∴OP=OQ.
∵∠A=60°,
∴∠POQ=360°﹣60°﹣90°﹣90°=120°.
∵∠DOE=120°,
∴∠POD=∠QOE.
∴△POD≌△QOE,
∴PD=EQ.
∴BD+CE=BP+PD+CE=BP+EQ+CE=BP+CQ=2BP=2×![]() OB=
OB=![]() BC.
BC.

(3)(2)中的结论不成立,线段BD、BC、CE之间的数量关系为BD﹣CE=![]() BC.
BC.
理由:如图3,过点O作OP⊥AB于P,作OQ⊥AC于Q,
则有∠OPD=∠OQE=90°.
由(1)知△OBP≌△OCQ,
∴BP=CQ,OP=OQ.
∵∠A=60°,
∴∠POQ=360°﹣60°﹣90°﹣90°=120°.
∵∠DOE=120°,
∴∠POD=∠QOE.
∴△POD≌△QOE,
∴PD=EQ.
在Rt△BOP中,∠B=60°,
∴BP=![]() OB=
OB=![]() BC
BC
∴BD﹣CE=BP+PD﹣CE=CQ+EQ﹣CE=CQ+CQ+CE﹣CE=2CQ=2BP=2×![]() BC=
BC=![]() BC.
BC.


【题目】某厂计划每天生产零件![]() 个,但实际每天生产量与计划量相比有出入. 下表是某周的生产情况(超产数量记为正、减产数量记为负):
个,但实际每天生产量与计划量相比有出入. 下表是某周的生产情况(超产数量记为正、减产数量记为负):
星期 | 一 | 二 | 三 | 四 | 五 | 六 | 日 |
增减 |
|
|
|
|
|
|
|
(1)由表可知该厂星期四生产零件 个,这周实际生产零件 个.(用含![]() 的代数式表示)
的代数式表示)
(2) 产量最高日比最低日多生产零件 个.
(3) 若该周厂计划每天生产零件数是![]() ,每个零件应支付工资
,每个零件应支付工资![]() 元,且每天超计划数的零件每个另奖
元,且每天超计划数的零件每个另奖![]() 元,那这周实际应支付工资多少元?
元,那这周实际应支付工资多少元?