题目内容
【题目】如图,正方形![]() 的边长为
的边长为![]() ,
, ![]() 、
、![]() 、
、![]() 、
、![]() 分别是
分别是![]() 、
、![]() 、
、![]() 、
、![]() 边上的动点(不含端点),且
边上的动点(不含端点),且![]() 、
、![]() 均过正方形的中心
均过正方形的中心![]() .
.
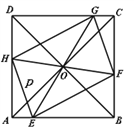
(1)填空: ![]()
![]() (“>”、“<”、“=”);
(“>”、“<”、“=”);
(2)当四边形![]() 为矩形时,请问线段
为矩形时,请问线段![]() 与
与![]() 应满足什么数量关系;
应满足什么数量关系;
(3)当四边形![]() 为正方形时,
为正方形时, ![]() 与
与![]() 交于点
交于点![]() ,求
,求![]() 的最小值.
的最小值.
【答案】(1)![]() ;(2)
;(2)![]() 或
或![]() ;(3)
;(3)![]() .
.
【解析】试题分析(1) 根据![]() 过正方形的中心
过正方形的中心![]() ,正方形是中心对称图形,所以OH=OF;
,正方形是中心对称图形,所以OH=OF;
(2)根据一线三等角证得![]() ∽
∽![]() ,
, ![]() ,
, ![]() ,依据
,依据![]() 求得x和y的函数关系式,从而找到
求得x和y的函数关系式,从而找到![]() 与
与![]() 的数量关系.
的数量关系.
(3) 当四边形![]() 为正方形时,证得
为正方形时,证得![]() ∽
∽![]() ,得到
,得到![]() ,从而
,从而![]() ,再证
,再证![]() ∽
∽![]() ,得到
,得到![]() ,因此当
,因此当![]() 最小时,即
最小时,即![]() 为垂线段时,
为垂线段时, ![]() 最小,计算即可求出最小值.
最小,计算即可求出最小值.
试题解析:
(1)![]()
(2)当四边形![]() 为矩形时,
为矩形时, ![]()
∴![]()
在正方形![]() 中,
中, ![]()
∴![]()
∴![]()
∴![]() ∽
∽![]()
∴![]()
令![]() ,
, ![]() ,显然
,显然![]()
得到![]()
∴![]() 或
或![]()
∴![]() 或
或![]()
(3)当四边形![]() 为正方形时,
为正方形时, ![]()
∴![]()
∴![]()
∵![]()
∴![]() ∽
∽![]()
∴![]() ,即
,即![]()
∴![]()
∵![]() ,
, ![]()
∴![]() ∽
∽![]()
∴![]() 即
即![]()
∴![]()
因此当![]() 最小时,即
最小时,即![]() 为垂线段
为垂线段![]() 时,
时, ![]() 最小,且等于
最小,且等于![]() .
.
点睛: 本题四边形综合问题,涉及相似三角形的判定与性质,正方形的判定与性质勾股定理等知识.解题的关键是利用相似三角形的对应边成比例进行线段的等量代换,利用分类讨论的数学思想解答本题,属于中考压轴题.

练习册系列答案
 导学全程练创优训练系列答案
导学全程练创优训练系列答案
相关题目