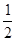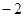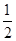题目内容
有一组等式: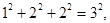
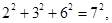
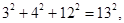
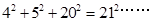 请观察它们的构成规律,用你发现的规律解答下面的问题:
请观察它们的构成规律,用你发现的规律解答下面的问题:
(1)写出第8个等式为 ;
(2)试用含正整数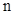 的等式表示你所发现的规律;
的等式表示你所发现的规律;
(3)说明你在(2)中所写等式成立的理由.
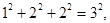
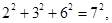
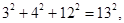
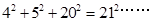 请观察它们的构成规律,用你发现的规律解答下面的问题:
请观察它们的构成规律,用你发现的规律解答下面的问题:(1)写出第8个等式为 ;
(2)试用含正整数
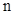 的等式表示你所发现的规律;
的等式表示你所发现的规律;(3)说明你在(2)中所写等式成立的理由.
(1)82+92+722=732;(2)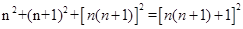 (n为正整数)(3)证明见解析.
(n为正整数)(3)证明见解析.
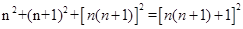 (n为正整数)(3)证明见解析.
(n为正整数)(3)证明见解析.试题分析:(1)观察不难发现,两个连续自然数的平方和加上它们积的平方,等于比它们的积大1的数的平方,然后写出即可.
(2)找到规律后,即可用含有n的等式来表示规律;
(3)证明左边=右边即可.
试题解析:(1)∵12+22+22=32,22+32+62=72,32+42+122=132,42+52+202=212,…,
∴第8个等式为:82+92+(8×9)2=(8×9+1)2,
即82+92+722=732
(2)
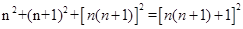 (n为正整数)
(n为正整数)(3)理由:∵
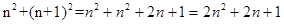
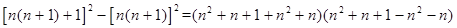
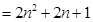
∴
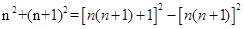
即:
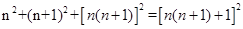
∴(2)中的等式成立.

练习册系列答案
 亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案
相关题目
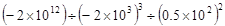
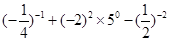
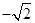
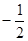 的绝对值是( )
的绝对值是( )