题目内容
【题目】如图，在△ABC中，AB=c，AC=b．AD是△ABC的角平分线，DE⊥A于E，DF⊥AC于F，EF与AD相交于O，已知△ADC的面积为1．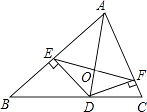
（1）证明：DE=DF；
（2）试探究线段EF和AD是否垂直？并说明理由；
（3）若△BDE的面积是△CDF的面积2倍．试求四边形AEDF的面积．
【答案】
（1）
证明：
∵AD是△ABC的角平分线，DE⊥A于E，DF⊥AC于F，
∴DE=DF（角平分线的性质）
（2）
解：垂直．理由如下：
∵AD是△ABC的角平分线，
∴∠EAD=∠FAD，
∵DE⊥AB，DF⊥AC，
∴∠AED=∠AFD=90°，
在Rt△AED和Rt△AFD中
，
∴Rt△AED≌Rt△AFD（AAS），
∴AE=AF，
∴点A在线段EF的垂直平分线上，
同理点D也在线段EF的垂直平分线上，
∴AD⊥EF
（3）
解：设S△CDF=x，则S△BDE=2x，
∵S△ACD=1，且△AED≌△AFD，
∴S△AED=S△AFD=1﹣x，
∴S△ABD=S△BDE+S△AED=2x+1﹣x=x+1，
又S△ABD= 
ABDE，S△ACD= ACDF，且AB=c，AC=b，
∴ ×cDE=x+1， ×bDF=1，
∴DE= 
，DF= 
，
又由（1）可知DE=DF，
∴ = ，解得x= 
﹣1，
∵△AED≌△AFD，
∴S△AED=S△AFD=S△ACD﹣S△CDF=1﹣x，
∴S四边形AEDF=2S△AED=2（1﹣x）=2[1﹣（ ﹣1）]=4﹣ 
，
即四边形AEDF的面积为4﹣
【解析】（1）由角平分线的性质直接可得到DE=DF；（2）可证明△AED≌△AFD，可知AE=AF，利用线段垂直平分线的判定可证明AD是EF的垂直平分线，可证得结论；（3）设△CDF的面积为x，则可分别表示出△BED、△ADE的面积，利用三角形的面积可分别表示出DE和DF，根据DE=DF可得到关于x的方程，可求得x的值，进一步可求得四边形AEDF的面积．
