Question

求值：
（1）cos60°+sin²45°-tan34°•tan56°；
（2）已知tanA=2，求

2sinA-cosA

4sinA+5cosA

的值．

Answer 1

分析：（1）根据特殊角的三角函数值及互余两角三角函数值相互间的关系计算．
（2）根据同角三角函数值相互间的关系计算．

解答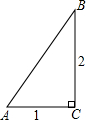：解：（1）原式=

1

2

+（

2

2

）²-1=

1

2

+

1

2

-1=0

（2）如图，∵tanA=2，
∴令AC=1，BC=2，则AB=

12+22

=

5

则sinA=

2

5

；cosA=

1

5

．
原式=

4 5 - 1 5

8 5 + 5 5

=

3

13

．

点评：本题考查特殊角三角函数值的计算，特殊角三角函数值计算在中考中经常出现，题型以选择题、填空题为主．
【相关链接】特殊角三角函数值：
（1）sin30°=

1

2

，cos30°=

3

2

，tan30°=

3

3

，cot30°=

3

；
sin45°=

2

2

，cos45°=

2

2

，tan45°=1，cot45°=1；
sin60°=

3

2

，cos60°=

1

2

，tan60°=

3

，cot60°=

3

3

．
（2）tanA•tan（90°-A）=1．