题目内容
(12分)如图,已知∠ACB=90°,AC=BC,BE⊥CE于E,AD⊥CE于D,CE与AB相交于F.
(1)求证:△CEB≌△ADC;
 (2)若AD=9cm,DE=6cm,求BE及EF的长.
(2)若AD=9cm,DE=6cm,求BE及EF的长.
证明:(1)∵B E⊥C E于E,AD⊥CE于D,
∴∠E=∠ADC=90°(1分)
∠BCE=90°— ∠ACD,∠CAD=90°¾∠ACD,
∴∠BCE=∠CAD (3分)
在△BCE与△CAD 中,
∠E=∠ADC,∠BCE=∠CAD, BC = AC ∴△C E B≌△AD C (4分)
(2)∵△C E B≌△AD C ∴ B E= D C, C E= AD
又AD=9 ∴C E= AD=9,D C= C E — D E= 9—6 = 3,∴B E= DC =3( cm) (5分)
∵∠E=∠ADF=90°,∠B FE=∠AFD,∴△B FE∽△ AFD (6分)
∴![]() 即有
即有 ![]() (7分)
(7分)
解得:EF=![]() ( cm) (8分)
( cm) (8分)
解析:略

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 x+b相交于点B、C,直线y=
x+b相交于点B、C,直线y=

 交坐标轴于A、B点,以线段AB为边向上作正方形ABCD,过点A、D、C的抛物线与直线的另一个交点为E.
交坐标轴于A、B点,以线段AB为边向上作正方形ABCD,过点A、D、C的抛物线与直线的另一个交点为E.
 轴上时停止,则抛物线上C、E两点间的抛物线所扫过的面积为 .
轴上时停止,则抛物线上C、E两点间的抛物线所扫过的面积为 .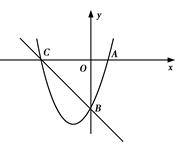
 的图象于点A、B,交x轴于点C.
的图象于点A、B,交x轴于点C.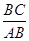 =
= ,求m的值和一次函数的解析式.
,求m的值和一次函数的解析式.