题目内容
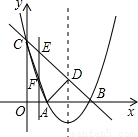
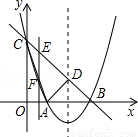
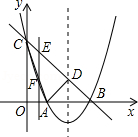 如图,顶点坐标为(2,-1)的抛物线y=ax2+bx+c(a≠0)与y轴交于点C(0,3),与x轴交于A、B两点.
如图,顶点坐标为(2,-1)的抛物线y=ax2+bx+c(a≠0)与y轴交于点C(0,3),与x轴交于A、B两点.(1)求抛物线的表达式;
(2)点E为直线BC上一动点,过点E作y轴的平行线EF,与抛物线交于点F.问是否存在点E,使得以D、E、F为顶点的三角形与△BCO相似?若存在,求点E的坐标;若不存在,请说明理由.
分析:(1)设抛物线的表达式为y=a(x-2)2-1(a≠0),将点C的坐标代入即可得出答案;
(2)由直线BC的解析式知,∠OBC=∠OCB=45°.又由题意知∠EFD=∠COB=90°,所以只有△EFD∽△COB.
(2)由直线BC的解析式知,∠OBC=∠OCB=45°.又由题意知∠EFD=∠COB=90°,所以只有△EFD∽△COB.
解答:解:(1)∵抛物线的顶点为(2,-1),
∴可设该函数解析式为:y=a(x-2)2-1(a≠0),
又∵抛物线y=ax2+bx+c(a≠0)与y轴交于点C(0,3),
∴3=a(0-2)2-1,
解得a=1,
∴该抛物线的解析式是y=(x-2)2-1(或y=x2-4x+3);
(2)假设存在点E,使得以D、E、F为顶点的三角形与△BCO相似.
由(1)知,该抛物线的解析式是y=x2-4x+3,即y=(x-1)(x-3),
∴该抛物线与x轴的交点坐标分别是A(1,0),B(3,0).
∵C(0,3),
∴易求直线BC的解析式为:y=-x+3.
∴∠OBC=∠OCB=45°.
又∵点D是对称轴上的一点,
∴D(2,1).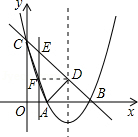
如图,连接DF.
∵EF∥y轴,
∴只有∠EFD=∠COB=90°.
∵以D、E、F为顶点的三角形与△BCO相似,
∴∠DEF=∠FDE=45°,
∴只有△EFD∽△COB.
设E(x,-x+3),则F(x,1),
∴1=x2-4x+3,
解得x=2±
,
∠EDF=90°;易知,直线AD:y=x-1,联立抛物线的解析式有:
x2-4x+3=x-1,解得 x1=1、x2=4;
当x=1时,y=-x+3=2;
当x=4时,y=-x+3=-1;
∴E3(1,2)、E4(4,-1).
∴E(2-
,1+
)或E′(2+
,1-
)或(1,2)或(4,-1).
∴可设该函数解析式为:y=a(x-2)2-1(a≠0),
又∵抛物线y=ax2+bx+c(a≠0)与y轴交于点C(0,3),
∴3=a(0-2)2-1,
解得a=1,
∴该抛物线的解析式是y=(x-2)2-1(或y=x2-4x+3);
(2)假设存在点E,使得以D、E、F为顶点的三角形与△BCO相似.
由(1)知,该抛物线的解析式是y=x2-4x+3,即y=(x-1)(x-3),
∴该抛物线与x轴的交点坐标分别是A(1,0),B(3,0).
∵C(0,3),
∴易求直线BC的解析式为:y=-x+3.
∴∠OBC=∠OCB=45°.
又∵点D是对称轴上的一点,
∴D(2,1).

如图,连接DF.
∵EF∥y轴,
∴只有∠EFD=∠COB=90°.
∵以D、E、F为顶点的三角形与△BCO相似,
∴∠DEF=∠FDE=45°,
∴只有△EFD∽△COB.
设E(x,-x+3),则F(x,1),
∴1=x2-4x+3,
解得x=2±
| 2 |
∠EDF=90°;易知,直线AD:y=x-1,联立抛物线的解析式有:
x2-4x+3=x-1,解得 x1=1、x2=4;
当x=1时,y=-x+3=2;
当x=4时,y=-x+3=-1;
∴E3(1,2)、E4(4,-1).
∴E(2-
| 2 |
| 2 |
| 2 |
| 2 |
点评:本题考查了二次函数综合题.解题时,利用了待定系数法求二次函数的解析式.注意解答(2)时,只有△EFD∽△COB一种情况.

练习册系列答案
相关题目
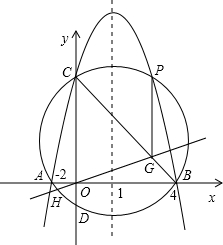 ⊙O′交y轴于另一点D,交抛物线于另一点P,过原点O且垂直于AD的直线交AD于点H,交BC于点G.
⊙O′交y轴于另一点D,交抛物线于另一点P,过原点O且垂直于AD的直线交AD于点H,交BC于点G.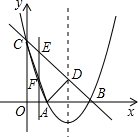 、B两点.
、B两点.