题目内容
【题目】在平面直角坐标系![]() 中,直线经过点A(-3,0),点B(0,
中,直线经过点A(-3,0),点B(0,![]() ),点P的坐标为(1,0),与
),点P的坐标为(1,0),与![]() 轴相切于点O,若将⊙P沿
轴相切于点O,若将⊙P沿![]() 轴向左平移,平移后得到(点P的对应点为点P′),当⊙P′与直线相交时,横坐标为整数的点P′共有( )
轴向左平移,平移后得到(点P的对应点为点P′),当⊙P′与直线相交时,横坐标为整数的点P′共有( )
A. 1个 B. 2个 C. 3个 D. 4个
【答案】C.
【解析】
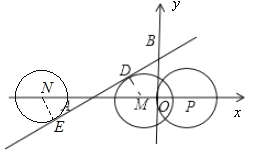
试题分析:如答图,∵点P的坐标为(1,0),⊙P与y轴相切于点O, ∴⊙P的半径是1,
若⊙P与AB相切时,设切点为D,
由点A(-3,0),点B(0,![]() ),∴OA=3,OB=
),∴OA=3,OB=![]() .∴AB=2
.∴AB=2![]() ,∠DAM=30°.
,∠DAM=30°.
设平移后圆与直线AB第一次相切时圆心为M(即对应的P′),∴MD⊥AB,MD=1.
又∵∠DAM=30°,∴AM=2,M点的坐标为(-1,0),即对应的P′点的坐标为(-1,0).
同理可得圆与直线第二次相切时圆心N的坐标为(-5,0).
∴当⊙P′与直线l相交时,横坐标为整数的点P′的横坐标可以是-2,-3,-4共三个.
故选C.

练习册系列答案
相关题目
