题目内容
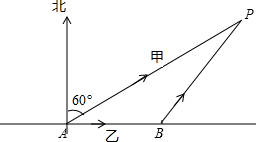
如图,甲、乙两辆货车于某日下午2:00同时从A地出发驶往P市,甲车沿一条公路向北偏东60°方向行驶,直达P市,其速度为30公里/小时;乙车先沿一条公路向正东方向行驶半小时后到达B地,卸下部分货物,再沿一条通向东偏北60°方向的公路驶往P市,其速度始终为40公里/小时.(1)设出发后经过t小时,甲车与P市的距离为s,求s与t之间的函数关系式,并写出自变量t的取值范围;
(2)已知在P市新建的移动通讯接收发射塔,其信号覆盖面积可达P市周围方圆30公里的区域(包括边缘地带),除此之外,该地区无其他发射塔,故甲、乙两车司机只能靠P市发射塔进行手机通话联系,问甲、乙两车司机从什么时刻开始可用手机取得联系(精确到分钟)?说明:手机联系必
 须是两人都在信号覆盖范围内方可进行,否则,手机无法联系.
须是两人都在信号覆盖范围内方可进行,否则,手机无法联系.
分析:(1)易知∠PAB=∠APB,即AB=PB,然后作PD⊥BC于D,求出PD长,再根据AP=
求出AP,从而求出s与t之间的函数关系式并写出自变量t的取值范围;
(2)若甲车司机手机要有信号,其距P必须等于或小于30千米,即让AP减去30千米再除以甲车的速度就可知道甲车司机手机什么时候有信号了,若乙车司机手机有信号,其距P必须等于或小于30千米,据此求出甲、乙两车司机从什么时刻开始可用手机取得联系.
| PD |
| sin30° |
(2)若甲车司机手机要有信号,其距P必须等于或小于30千米,即让AP减去30千米再除以甲车的速度就可知道甲车司机手机什么时候有信号了,若乙车司机手机有信号,其距P必须等于或小于30千米,据此求出甲、乙两车司机从什么时刻开始可用手机取得联系.
解答: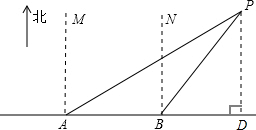 解:(1)作辅助线PD⊥BC于D;
解:(1)作辅助线PD⊥BC于D;
∵∠PBD=∠PAB+∠APB,∠PBD=60°,∠PAB=30°
∴∠APB=30°,即AB=PB=20(千米)
PD=PB×sin60°=20×
=10
(千米)
AP=
=20
(千米)
∴30t+s=20
,
即s与t之间的函数关系式为:s=20
-30t,
∴20
-30t≥0,
即t的取值范为:t≤
;
(2)∵其信号覆盖面积只可达P市周围方圆30千米的区域(包括边缘地带),除此以外,该地区无其他发射塔;
∴甲车司机有手机信号时间为从出发后
小时有信号,
(20
-30)÷30≈0.155(小时),合9分钟.
此时乙车司机手机也有信号,
因此出甲、乙两车司机从从出发9分钟开始可用手机取得联系.
 解:(1)作辅助线PD⊥BC于D;
解:(1)作辅助线PD⊥BC于D;∵∠PBD=∠PAB+∠APB,∠PBD=60°,∠PAB=30°
∴∠APB=30°,即AB=PB=20(千米)
PD=PB×sin60°=20×
| ||
| 2 |
| 3 |
AP=
| PD |
| sin30° |
| 3 |
∴30t+s=20
| 3 |
即s与t之间的函数关系式为:s=20
| 3 |
∴20
| 3 |
即t的取值范为:t≤
2
| ||
| 3 |
(2)∵其信号覆盖面积只可达P市周围方圆30千米的区域(包括边缘地带),除此以外,该地区无其他发射塔;
∴甲车司机有手机信号时间为从出发后
| AP-30 |
| 30 |
(20
| 3 |
此时乙车司机手机也有信号,
因此出甲、乙两车司机从从出发9分钟开始可用手机取得联系.
点评:本题考查了解直角三角形的应用,关键是在做题过程中可灵活选用三角函数去计算.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目

 须是两人都在信号覆盖范围内方可进行,否则,手机无法联系.
须是两人都在信号覆盖范围内方可进行,否则,手机无法联系. ,
, )
)
 ,
, )
)