题目内容
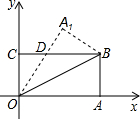 如图在直角坐标系中,将矩形OABC沿OB对折,使点A落在点A1处,OB=8,OC=4,则△BDO的面积为
如图在直角坐标系中,将矩形OABC沿OB对折,使点A落在点A1处,OB=8,OC=4,则△BDO的面积为10
10
.分析:根据折叠的性质得出BD=OD,设DO=DB=xcm,在RT△OCD中利用勾股定理即可得出BD的长度,因为OC为高,利用三角形的面积公式求出△BDO的面积.
解答:解:∵BC∥AO,
∴∠BOA=∠OBC,
根据翻折不变性得,∠A1OB=∠BOA,
∴∠OBC=∠A1OB,
∴DO=DB.
设DO=DB=xcm,
则CD=(8-x)cm,
又∵OC=4,
∴(8-x)2+42=x2,
解得x=5.
∴BD=5,
∴S△BDO=
×5×4=10;
故答案为:10.
∴∠BOA=∠OBC,
根据翻折不变性得,∠A1OB=∠BOA,
∴∠OBC=∠A1OB,
∴DO=DB.
设DO=DB=xcm,
则CD=(8-x)cm,
又∵OC=4,
∴(8-x)2+42=x2,
解得x=5.
∴BD=5,
∴S△BDO=
| 1 |
| 2 |
故答案为:10.
点评:本题考查了翻折变换、勾股定理及三角形的面积,解答本题的关键是得出DO=DB,利用勾股定理得出BD的长度,难度一般.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 24、(北师大版)如图在直角坐标系中,右边的图案是由左边的图案经过平移以后得到的.左图案中左右眼睛的坐标分别是(-4,2)、(-2,2),右图中左眼的坐标是(3,4),则右图案中右眼的坐标是
24、(北师大版)如图在直角坐标系中,右边的图案是由左边的图案经过平移以后得到的.左图案中左右眼睛的坐标分别是(-4,2)、(-2,2),右图中左眼的坐标是(3,4),则右图案中右眼的坐标是
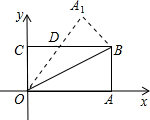 如图在直角坐标系中,将矩形OABC沿OB对折,使点A落在点A1处,OA=8,OC=4,则△BDO的面积为
如图在直角坐标系中,将矩形OABC沿OB对折,使点A落在点A1处,OA=8,OC=4,则△BDO的面积为
 如图在直角坐标系中,△AOB是等边三角形,若B点的坐标是(2,0),则A点的坐标是( )
如图在直角坐标系中,△AOB是等边三角形,若B点的坐标是(2,0),则A点的坐标是( )