��Ŀ����
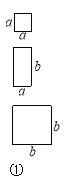
����Ŀ��һ�죬С����С����ֽƬƴͼ��Ϸ����������ͼ���е����ֲ��ϸ����ɿ���ƴ��һЩ������������ijЩ��ʽ������ͼ�����Խ���Ϊ����a+2b����a+b��=a2+3ab+2b2��
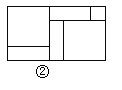
��1��ͼ�����Խ���Ϊ��ʽ��
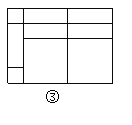
��2��Ҫʹƴ���ľ������Ϊ3a2+8ab+4b2�����˾��εij�Ϊ ����Ϊ ��
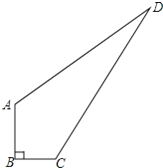
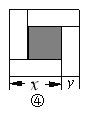
��3����ͼ�������������ı߳�Ϊm��С�����ε��߳�Ϊn������x��y��ʾ�ĸ����ε����߳���x>y�����۲�ͼ����ָ�����¹�ϵʽ
��. ![]() ��.x-y=n ��.
��.x-y=n ��.![]() ��
��![]()
��. ![]() ������ȷ���м����� ��
������ȷ���м����� ��
A��2�� B��3�� C��4�� D��5��
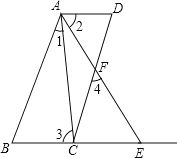
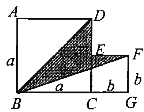
��4����ͼ5���ǽ������߳��ֱ�Ϊ![]() ��
��![]() ��������ƴ��һ��B��C��G������ͬһֱ���ϣ�����BD��BF�����������εı߳�����a+b=6��ab=6�����������Ӱ���ֵ����S�� ��
��������ƴ��һ��B��C��G������ͬһֱ���ϣ�����BD��BF�����������εı߳�����a+b=6��ab=6�����������Ӱ���ֵ����S�� ��
���𰸡���1����2a+b����a+2b��=2a2+5ab+2b2����2������3a+2b��������a+2b������3��D��
��4��9.
��������
�����������1�����ò���֮�͵������壬��ͼ�ο���һ�������dz�Ϊa+2b����2a+b��һ�������Σ�Ҳ�ɿ�������2���߳�Ϊa�������Σ���5����b��a�ij������Լ�2���߳�Ϊb����������ɵģ���2�����÷ֽ���ʽ��3a2+8ab+4b2�ֽ����������ʽ�ij˻����Ϳɵ������εij��Ϳ�����3������ͼ�ο��Է��ִ������εı߳�m����x+y����������ȷ������С�����εı߳�n����x-y��������ȷ������������������Ҳ��ȷ��������x2+2xy+y2=m2��������x2-2xy+y2=n2����ʽ��ӵõ���Ҳ��ȷ����ʽ����õ���Ҳ��ȷ.��ѡD��
��4����Ӱ���ֵ�������Կ�����һ����a+b����a�þ��μ�ȥ��b����a-b�ľ��Σ��ټ�ȥֱ�DZ߳�Ϊa�ĵ���ֱ�������Σ��ټ�ȥֱ�DZ�Ϊa+b��b��ֱ�������ε����.��������ʽ�������������ֵ.
��������� ��1����2a+b����a+2b��=2a2+5ab+2b2����2������3a+2b��������a+2b������3��D��
S��Ӱ=a��a+b��-b��a-b��-![]() a2-
a2-![]() b��a+b��=a2+ab-ab+b2-
b��a+b��=a2+ab-ab+b2-![]() a2-
a2-![]() b2-
b2-![]() ab=
ab=![]() ��a2+b2��-
��a2+b2��-![]() ab
ab
=![]() [��a+b��2-2ab] -
[��a+b��2-2ab] -![]() ab=
ab=![]() ����62-12��-
����62-12��-![]() ��6=12-3=9.����Ӱ���ֵ����Ϊ9.
��6=12-3=9.����Ӱ���ֵ����Ϊ9.

 ��������ϵ�д�
��������ϵ�д� ��ӡ�Ļ���ʱ����ϵ�д�
��ӡ�Ļ���ʱ����ϵ�д�