题目内容
 已知:如图,在平行四边形ABCD中,G、H分别是AD、BC的中点,E、F是对角线上的两点,且AE⊥BD,CF⊥BD,垂足分别为E、F.求证:四边形GEHF是平行四边形.
已知:如图,在平行四边形ABCD中,G、H分别是AD、BC的中点,E、F是对角线上的两点,且AE⊥BD,CF⊥BD,垂足分别为E、F.求证:四边形GEHF是平行四边形.考点:平行四边形的判定与性质
专题:证明题
分析:如图,连接GH交BD于点O.通过证明四边形GEHF的对角线互相平分来推知四边形GEHF是平行四边形.
解答: 证明:如图,连接GH交BD于点O.
证明:如图,连接GH交BD于点O.
∵四边形ABCD是平行四边形,
∴OB=OD,AB=CD,AB∥CD.
∵G、H分别是AD、BC的中点,
∴GH∥AB∥CD,
∴GO=
AB,HO=
CD,
∴GO=HO.
∵AB∥CD,
∴∠1=∠2,
由∵AE⊥BD,CF⊥BD,
∴∠AEB=∠CFD=90°.
∴在△ABE与△CDF中,
,
∴△ABE≌△CDF(AAS),
∴BE=DF,
∴OB-BE=OD-DF,即OE=OF,
∴四边形GEHF是平行四边形.
 证明:如图,连接GH交BD于点O.
证明:如图,连接GH交BD于点O.∵四边形ABCD是平行四边形,
∴OB=OD,AB=CD,AB∥CD.
∵G、H分别是AD、BC的中点,
∴GH∥AB∥CD,
∴GO=
| 1 |
| 2 |
| 1 |
| 2 |
∴GO=HO.
∵AB∥CD,
∴∠1=∠2,
由∵AE⊥BD,CF⊥BD,
∴∠AEB=∠CFD=90°.
∴在△ABE与△CDF中,
|
∴△ABE≌△CDF(AAS),
∴BE=DF,
∴OB-BE=OD-DF,即OE=OF,
∴四边形GEHF是平行四边形.
点评:本题考查了平行四边形的判定与性质.平行四边形的判定方法共有五种,应用时要认真领会它们之间的联系与区别,同时要根据条件合理、灵活地选择方法.

练习册系列答案
相关题目
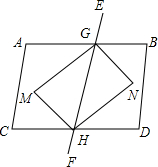 平行四边形ABCD中,AB∥CD,GM、GN、HM、HN分别平分∠AGH、∠BGH、∠CHG、∠DHG,试判断四边形GMHN的形状,并说明你的理由.
平行四边形ABCD中,AB∥CD,GM、GN、HM、HN分别平分∠AGH、∠BGH、∠CHG、∠DHG,试判断四边形GMHN的形状,并说明你的理由.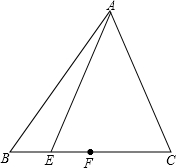 数学课上,神奇而有魔力的黄金分割点激起了同学们极大的兴趣,某学习兴趣小组在探究该知识时,由黄金分割点联想到黄金分割线,类似的给出定义:直线AB将一个面积为S的图形分成两部分,这两部分的面积分别为S1和S2,如果S1:S2=S1:S(S1>S2),那么称直线AB为该图的黄金分割线.
数学课上,神奇而有魔力的黄金分割点激起了同学们极大的兴趣,某学习兴趣小组在探究该知识时,由黄金分割点联想到黄金分割线,类似的给出定义:直线AB将一个面积为S的图形分成两部分,这两部分的面积分别为S1和S2,如果S1:S2=S1:S(S1>S2),那么称直线AB为该图的黄金分割线. 如图,在边长为1的小正方形组成的网格中,△AOB的三个顶点均在格点上,点O为原点,点A、B的坐标分别为(-2,3)和(-3,1),AB=
如图,在边长为1的小正方形组成的网格中,△AOB的三个顶点均在格点上,点O为原点,点A、B的坐标分别为(-2,3)和(-3,1),AB=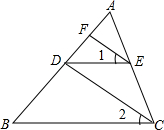 如图,已知EF∥CD,∠1=∠2,你能找到DE平行于BC的理由吗?
如图,已知EF∥CD,∠1=∠2,你能找到DE平行于BC的理由吗?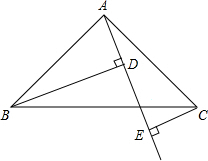 如图,在Rt△ABC中,∠BAC=90°,AB=AC,AE是过A点的一条直线,且B点和C点在AE的两侧,BD⊥AE于点D,CE⊥AE于点E,CE=2,BD=6,求DE的长.
如图,在Rt△ABC中,∠BAC=90°,AB=AC,AE是过A点的一条直线,且B点和C点在AE的两侧,BD⊥AE于点D,CE⊥AE于点E,CE=2,BD=6,求DE的长. 如图,已知⊙O1、⊙O2外切于点P,AB是一条外公切线,A、B为切点.
如图,已知⊙O1、⊙O2外切于点P,AB是一条外公切线,A、B为切点.