题目内容
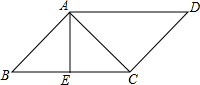如图，在平行四边形ABCD中，已知AC⊥CD，AE⊥BC，若∠EAC=50°，求∠D的度数．考点：平行四边形的性质
专题：
分析：首先求出∠ACDA的度数，因为AC⊥CD，所以∠ACD=90°，进而求出∠BCD的度数，利用平行四边形的性质：邻角互补即可求出∠D的度数．
解答：解：∵AE⊥BC，
∴∠AEC=90°，
∵∠EAC=50°，
∴∠BCD=40°，
∵AC⊥CD，
∴∠ACD=90°，
∴∠BCD=130°，
∵四边形ABCD是平行四边形，
∴∠D=50°．
∴∠AEC=90°，
∵∠EAC=50°，
∴∠BCD=40°，
∵AC⊥CD，
∴∠ACD=90°，
∴∠BCD=130°，
∵四边形ABCD是平行四边形，
∴∠D=50°．
点评：本题考查了垂直的定义、三角形的内角和定理以及平行四边形的性质，题目比较简单，属于基础性题目．
练习册系列答案
阅读快车系列答案
相关题目
方程mx2+3x-5=0是关于x的一元二次方程，则m的取值（ ）
| A、m≥0 | B、m≤0 |
| C、m取任意实数 | D、m≠0 |
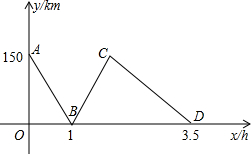如图，甲、丙两地相距500km，一列快车从甲地驶往丙地且途中经过乙地，一列慢车从乙地驶往丙地，两车同时出发同向而行，设慢车行驶的时间为x（h），两车之间的距离为y（km），图中的折线表示y与x之间的函数关系，根据图象进行以下探究．
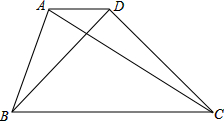如图，已知梯形ABCD中，AD∥CB，AD=1，BC=4，BD=3，AC=4，求梯形ABCD面积．