题目内容
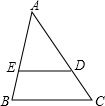 如图,可得出DE∥BC的条件是
如图,可得出DE∥BC的条件是
- A.∠ACB=∠BAD
- B.∠ABC=∠ADE
- C.∠ABC=180°-∠BED
- D.∠ACB=180°-∠BAD
C
分析:结合图形分析两角的位置关系,根据平行线的判定方法判断.
解答:A、∵∠ACB与∠BAD不是DE与BC被AC所截形成的角,故推不出DE∥BC,故错误;
B、∠ABC与∠ADE不是同位角,所以不能判断DE∥BC,故错误;
C.∵∠ABC+∠BED=180°,∴DE∥BC(同旁内角互补,两直线平行),故正确;
D、∵∠ACB+∠BAD=180°,∴AB∥BC(同旁内角互补,两直线平行),故错误.
故选C.
点评:在复杂的图形中具有相等关系的两角首先要判断它们是否是同位角或内错角,及同旁内角互补的等式变形,被判断平行的两直线是否由“三线八角”而产生的被截直线.
分析:结合图形分析两角的位置关系,根据平行线的判定方法判断.
解答:A、∵∠ACB与∠BAD不是DE与BC被AC所截形成的角,故推不出DE∥BC,故错误;
B、∠ABC与∠ADE不是同位角,所以不能判断DE∥BC,故错误;
C.∵∠ABC+∠BED=180°,∴DE∥BC(同旁内角互补,两直线平行),故正确;
D、∵∠ACB+∠BAD=180°,∴AB∥BC(同旁内角互补,两直线平行),故错误.
故选C.
点评:在复杂的图形中具有相等关系的两角首先要判断它们是否是同位角或内错角,及同旁内角互补的等式变形,被判断平行的两直线是否由“三线八角”而产生的被截直线.

练习册系列答案
相关题目
 4、如图,可得出DE∥BC的条件是( )
4、如图,可得出DE∥BC的条件是( )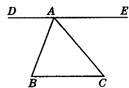 20、如图所示,可得出DE∥BC的条件:(1)∠ABC+∠
20、如图所示,可得出DE∥BC的条件:(1)∠ABC+∠