Question

将半径为10cm，弧长为10π的扇形围成圆锥（接缝忽略不计），那么圆锥的母线与圆锥底面的夹角的正弦值是________．

Answer 1

分析：利用扇形的弧长和母线长求得扇形的弧长，并利用圆锥的底面周长等于展开扇形的弧长求得圆锥的底面半径，在根据圆锥的母线长、底面半径及高围成直角三角形，利用勾股定理求得高，用高除以母线长即可得到正弦值．
解答：∵扇形的半径为10，弧长为10π，
∴圆锥的底面半径r=10π÷2π=5，
∵圆锥的母线长、底面半径及高围成直角三角形，
∴圆锥的高为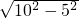：=5，
∴圆锥的母线与圆锥底面的夹角的正弦值是 =，
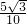故答案为：．
点评：本题考查了圆锥的侧面展开图与圆锥的关系，解题的关键是弄清这个关系，这也是同学们学习的难点．