题目内容
(2007•济宁)如图,从P点引⊙O的两切线PA、PA、PB,A、B为切点,已知⊙O的半径为2,∠P=60°,则图中阴影部分的面积为 .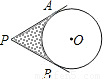
【答案】分析:如果连接OA、OB、OP,那么阴影部分的面积可以用两个直角三角形的面积和圆心角为120°的扇形的面积差来求得.
解答: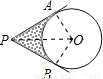 解:连接OA,OB,OP,则∠OAP=∠OBP=90°,
解:连接OA,OB,OP,则∠OAP=∠OBP=90°,
∴∠AOB=180°-60°=120°,∠AOP=∠BOP=60°;
由切线长定理知,AP=PB=AOtan60°=2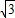 ,
,
∴S阴影=S△APO+S△OPB-S扇形OAB;
即:S阴影=2× ×OA•AP-
×OA•AP-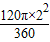 =4
=4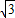 -
- π.
π.
点评:本题考查了切线长定理以及直角三角形、扇形的面积的求法.
解答:
 解:连接OA,OB,OP,则∠OAP=∠OBP=90°,
解:连接OA,OB,OP,则∠OAP=∠OBP=90°,∴∠AOB=180°-60°=120°,∠AOP=∠BOP=60°;
由切线长定理知,AP=PB=AOtan60°=2
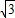 ,
,∴S阴影=S△APO+S△OPB-S扇形OAB;
即:S阴影=2×
 ×OA•AP-
×OA•AP-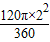 =4
=4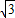 -
- π.
π.点评:本题考查了切线长定理以及直角三角形、扇形的面积的求法.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
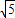 时,试求出m的取值范围;
时,试求出m的取值范围;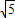 时,你认为m的取值范围如何?(只要求写出结论)
时,你认为m的取值范围如何?(只要求写出结论)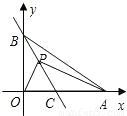
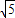 时,试求出m的取值范围;
时,试求出m的取值范围;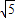 时,你认为m的取值范围如何?(只要求写出结论)
时,你认为m的取值范围如何?(只要求写出结论)
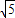 时,试求出m的取值范围;
时,试求出m的取值范围;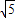 时,你认为m的取值范围如何?(只要求写出结论)
时,你认为m的取值范围如何?(只要求写出结论)
 ,求⊙O的直径.
,求⊙O的直径.