题目内容
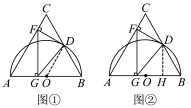
【题目】如图,已知等边△ABC,AB=12,以AB为直径的半圆与BC边交于点D,过点D作DF⊥AC,垂足为F,过点F作FG⊥AB,垂足为G,连结GD.
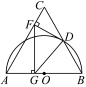
(1)求证:DF是⊙O的切线;
(2)求FG的长;(3)求tan∠FGD的值.
【答案】(1)证明过程见解析;(2)![]() ;(3)
;(3)![]()
【解析】
试题分析:(1)连接OD,根据等边三角形得出∠A=∠B=∠C=60°,根据OD=OB得到∠ODB=60°,得到OD∥AC,根据垂直得出切线;(2)根据中位线得出BD=CD=6,根据Rt△CDF的三角函数得出CF的长度,从而得到AF的长度,最后根据Rt△AFG的三角函数求出FG的长度;(3)过点D作DH⊥AB,根据垂直得出FG∥DH,根据Rt△BDH求出BH、DH的长度,然后得出∠GDH的正切值,从而得到∠FGD的正切值.
试题解析:(1)如图①,连结OD, ∵△ABC为等边三角形, ∴∠C=∠A=∠B=60°,
而OD=OB, ∴△ODB是等边三角形,∠ODB=60°, ∴∠ODB=∠C,
∴OD∥AC, ∵DF⊥AC,∴OD⊥DF,∴DF是⊙O的切线
(2)∵OD∥AC,点O为AB的中点,∴OD为△ABC的中位线,
∴BD=CD=6.在Rt△CDF中,∠C=60°,∴∠CDF=30°,
∴CF=CD=3,∴AF=AC-CF=12-3=9 在Rt△AFG中,∵∠A=60°,∴FG=AF·sinA=9×=
(3)如图②,过D作DH⊥AB于H.∵FG⊥AB,DH⊥AB,∴FG∥DH,∴∠FGD=∠GDH.在Rt△BDH中,∠B=60°,∴∠BDH=30°,∴BH=BD=3,DH=BH=3.∴tan∠GDH===,
∴tan∠FGD=tan∠GDH=

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目