题目内容
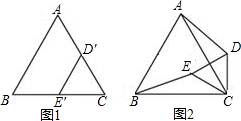
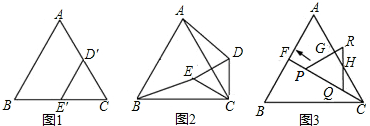
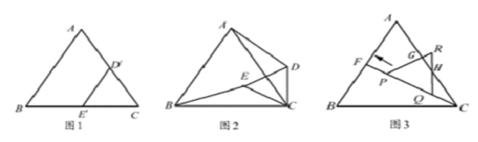
如图1，是边长分别为4和3的两个等边三角形纸片ABC和CD′E′叠放在一起．
（1）操作：固定△ABC，将△CD′E′绕点C顺时针旋转得到△CDE，连接AD、BE，如图2．探究：在图2中，线段BE与AD之间有怎样的大小关系？试说明理由；
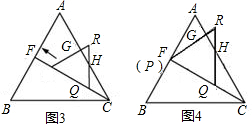
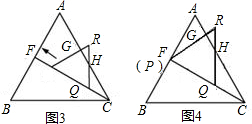
（2）操作：固定△ABC，若将△CD′E′绕点C顺时针旋转30°得到△CDE，连接AD、BE，CE的延长线交AB于点F，在线段CF上沿着CF方向以每秒1个单位长的速度平移，平移后的△CDE设为△PQR，如图3．探究：在图3中，除△ABC和△CDE外，还有哪个三角形是等腰三角形？写出你的结论并说明理由；
（3）探究：如图4，在（2）的条件下，将△PQR的顶点P移动至F点，求此时QH的长度．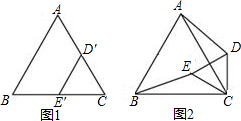
解：（1）BE=AD
证明：由题意可得，BC=AC，CE=CD，
∵∠BCE+∠ACE=60°∠ACE+∠ACD=60°
∴∠BCE=∠ACD，
∴△BCE≌△ACD，
∴BE=AD．
（2）△HQC为等腰三角形
证明：因为∠FCB=30°，
所以∠ACF=30°，
又因为∠RQP=60°，
所以∠QHC=∠HCQ=30°，
所以△HQC为等腰三角形；
（3）由题意得，AF=2，在Rt△AFG中，FG=
，所以GR=3-，
在Rt△GRH中，RH=2（3-），
所以HQ=3-2（3-）=2-3
分析：（1）求两条线段之间的关系，可先证明△BCE≌△ACD，进而得出两条线之间的关系．
（2）等腰三角形的判定问题，可根据题中角之间的关系进行判断．
（3）简单的计算问题，在直角三角形中，利用勾股定理求解即可．
点评：本题考查了等腰三角形的性质及判定定理轴对称的性质及平移的性质；进行角的等量代换是正确解答本题的关键．
证明：由题意可得，BC=AC，CE=CD，
∵∠BCE+∠ACE=60°∠ACE+∠ACD=60°
∴∠BCE=∠ACD，
∴△BCE≌△ACD，
∴BE=AD．
（2）△HQC为等腰三角形
证明：因为∠FCB=30°，
所以∠ACF=30°，
又因为∠RQP=60°，
所以∠QHC=∠HCQ=30°，
所以△HQC为等腰三角形；
（3）由题意得，AF=2，在Rt△AFG中，FG=
，所以GR=3-，在Rt△GRH中，RH=2（3-
），所以HQ=3-2（3-
）=2-3分析：（1）求两条线段之间的关系，可先证明△BCE≌△ACD，进而得出两条线之间的关系．
（2）等腰三角形的判定问题，可根据题中角之间的关系进行判断．
（3）简单的计算问题，在直角三角形中，利用勾股定理求解即可．
点评：本题考查了等腰三角形的性质及判定定理轴对称的性质及平移的性质；进行角的等量代换是正确解答本题的关键．
练习册系列答案
相关题目
