题目内容
【题目】如图,△ABC和△ADC分别在AC的两侧,∠BAC:∠B:∠ACB=4:3:2,且∠DAC=40°. 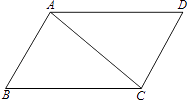
(1)试说明AD∥BC.
(2)若AB与CD也平行,求∠D的度数.
【答案】
(1)解:∵∠BAC:∠B:∠ACB=4:3:2,
∴∠ACB=180°× ![]() =40°,
=40°,
∠BAC=180°× ![]() =80°,
=80°,
∵∠DAC=40°,
∴∠DAC=∠ACB,
∴AD∥BC
(2)解:∵AB∥CD,
∴∠D+∠DAB=180°,
∵∠DAB=∠DAC+∠BAC=120°,
∴∠D=60°
【解析】(1)根据已知条件得到∠ACB=180°× ![]() =40°,∠BAC=180°×
=40°,∠BAC=180°× ![]() =80°,于是得到∠DAC=∠ACB,根据平行线的判定定理即可得到结论;(2)根据平行线的性质得到∠D+∠DAB=180°,由三角形的外角的性质得到∠DAB=∠DAC+∠BAC=120°,即可得到结论.
=80°,于是得到∠DAC=∠ACB,根据平行线的判定定理即可得到结论;(2)根据平行线的性质得到∠D+∠DAB=180°,由三角形的外角的性质得到∠DAB=∠DAC+∠BAC=120°,即可得到结论.
【考点精析】认真审题,首先需要了解平行线的判定与性质(由角的相等或互补(数量关系)的条件,得到两条直线平行(位置关系)这是平行线的判定;由平行线(位置关系)得到有关角相等或互补(数量关系)的结论是平行线的性质).

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目