题目内容
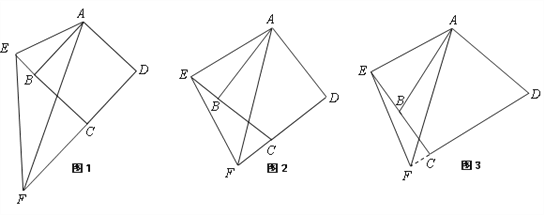
【题目】如图1，四边形ABCD，将顶点为A的角绕着顶点A顺时针旋转，若角的一条边与DC的延长线交于点F，角的另一条边与CB的延长线交于点E，连接EF．
●特例发现 若四边形ABCD为正方形，当∠EAF＝45°时，则EF、DF、BE满足数量关系为 ；
●深入探究 如图2，如果在四边形ABCD中，AB＝AD，∠ABC＝∠ADC＝90°，当∠EAF＝
∠BAD时，则EF、DF、BE满足数量关系为 ；
如图3，如果四边形ABCD中，AB＝AD，∠ABC与∠ADC互补，当∠EAF＝
∠BAD 时，EF与DF、BE之间的数量关系是否发生改变？请给出详细的证明过程；
●拓展应用 在（3）中，若BC=4，DC=7，CF=2，求△CEF的周长．
【答案】●特例发现， EF＝DF－BE；●深入探究 ，EF=DF－BE；EF＝DF－BE，证明见解析；●拓展应用△CEF的周长为15．
【解析】试题分析：“特例发现”与” “深入探究”解题思路一致，都是通过两步全等来实现；在DC上截取DG=BE，第一步，首先证△ADG≌△ABE，得AE=AG；第二步，证△AGF≌△AEF，得EF=GF，由此得到DF、EF、BE的数量关系．
根据前三问的结论知：EF=DF-BE，那么△CEF的周长可转化为：CE＋EF＋FC＝CE＋（DF－BE）＋FC ＝BC＋DC＋2FC，从而得解．
试题解析：●特例发现 EF＝DF－BE；
●深入探究 EF=DF－BE，
如图4，在DC上截取DG，使DG=BE，连接AG．
∵∠D+∠ABC＝180°,∠ABC+∠ABE＝180°，
∴∠ABE＝∠D．
又∵AB＝AD，DG=BE，
∴△ABE≌△ADG（SAS）．
∴∠BAE＝∠DAG，AE＝AG．
又∵∠DAG＋∠BAF＝∠BAE＋∠BAF＝∠EAF＝
∠BAD，
∴∠GAF＝∠BAD－（∠DAG＋∠BAF）＝
∠BAD，
∴∠GAF=∠EAF．
∵AE＝AG （前面已证），AF＝AF，
∴△AFE≌△AFG（SAS），
∴EF＝GF．
∴EF＝GF＝DF－DG＝DF－BE．
●拓展应用
△CEF的周长：CE＋EF＋FC＝CE＋（DF－BE）＋FC
＝（CE－BE）＋DF＋FC
＝（CE－BE）＋（DC＋FC）＋FC
＝BC＋DC＋2FC
＝4＋7＋2×2
＝15．
