题目内容
如图,四边形ABCD是菱形,∠ABC=120°AD=2,则对角线AC的长是( )

| A.4 | B. | C. | D. |

D
根据∠ABC=120°,可得出△ADB是等边三角形,从而可求出BD的长,根据菱形的对角线互相平分可求出DO,在RT△ADO中利用勾股定理可得出AO的长,进而可得出对角线AC的长.
解:∵∠ABC=120°,
∴∠DAB=60°,
∴△ADB是等边三角形,
故可得BD=AD=2,DO=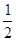 BD=1,
BD=1,
在RT△ADO中,AD2=DO2+AO2,
∴OA=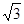 ,
,
即可求出对角线AC=2AO=2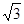 .
.
故选D.
本题考查菱形的性质及勾股定理的知识,属于中档题,掌握菱形的四边相等及对角线互相垂直且平分是解答本题的关键.
解:∵∠ABC=120°,
∴∠DAB=60°,
∴△ADB是等边三角形,
故可得BD=AD=2,DO=
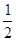 BD=1,
BD=1,在RT△ADO中,AD2=DO2+AO2,
∴OA=
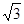 ,
,即可求出对角线AC=2AO=2
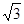 .
.故选D.
本题考查菱形的性质及勾股定理的知识,属于中档题,掌握菱形的四边相等及对角线互相垂直且平分是解答本题的关键.

练习册系列答案
 七彩题卡口算应用一点通系列答案
七彩题卡口算应用一点通系列答案
相关题目
 ,点
,点 是
是 的中点,点
的中点,点 是
是 上的一点,
上的一点, ,现沿直线
,现沿直线 将纸片折叠,使点
将纸片折叠,使点 落在纸片上的点
落在纸片上的点 处,连结
处,连结 ,则与
,则与 相等的角的个数为 【 】
相等的角的个数为 【 】 


 CD中,AD=4,BC=9,∠
CD中,AD=4,BC=9,∠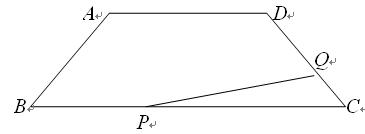



 上.
上. ,求tan∠EBC的值.
,求tan∠EBC的值.