ЬтФПФкШн
ЁОЬтФПЁПЙцЖЈЃКЧѓШєИЩИіЯрЭЌЕФгаРэЪ§ЃЈОљВЛЕШгк ![]() ЃЉЕФГ§ЗЈдЫЫуНазіГ§ЗНЃЌШч
ЃЉЕФГ§ЗЈдЫЫуНазіГ§ЗНЃЌШч ![]() ЃЌ
ЃЌ ![]() ЕШЃЌРрБШгаРэЪ§ГЫЗНЃЌЮвУЧАб
ЕШЃЌРрБШгаРэЪ§ГЫЗНЃЌЮвУЧАб ![]() МЧзї
МЧзї ![]() ЃЌЖСзїЁА
ЃЌЖСзїЁА ![]() ЕФШІ
ЕФШІ ![]() ДЮЗНЃЌЁБ
ДЮЗНЃЌЁБ ![]() МЧзї
МЧзї ![]() ЃЌЖСзїЃКЁА
ЃЌЖСзїЃКЁА ![]() ЕФШІ
ЕФШІ ![]() ДЮЗНЁБ.вЛАуЕиЃЌАб
ДЮЗНЁБ.вЛАуЕиЃЌАб ![]() МЧзїa ЃЌ ЖСзїЁА
МЧзїa ЃЌ ЖСзїЁА ![]() ЕФШІ
ЕФШІ ![]() ДЮЗНЁБ
ДЮЗНЁБ
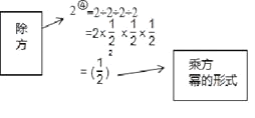
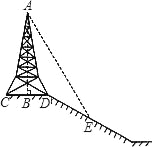
ЃЈ1ЃЉЃЈГѕВНЬНОПЃЉ
Ђё.жБНгаДГіМЦЫуНсЙћЃК ![]() =________ЃЌ
=________ЃЌ ![]() ________.
________.
Ђђ.ЙигкГ§ЗНЃЌЯТСаЫЕЗЈДэЮѓЕФЪЧЃЈ________ЃЉ
A.ШЮКЮЗЧСуЪ§ЕФШІ ![]() ДЮЗНЖМЕШгкЫќЕФЕЙЪ§
ДЮЗНЖМЕШгкЫќЕФЕЙЪ§
B.СНИіЪ§ЛЅЮЊЕЙЪ§ЃЌФЧУДЫќЕФnДЮЗНКЭШІnДЮЗНвВЛЅЮЊЕЙЪ§
C.ЖдгкШЮКЮе§ећЪ§ ![]() ЃЌ(-1)=1
ЃЌ(-1)=1
D.ИКЪ§ЕФШІЦцЪ§ДЮЗННсЙћЪЧИКЪ§ЃЌИКЪ§ЕФШІХМЪ§ДЮЗННсЙћЪЧе§Ъ§.
ЃЈ2ЃЉЃЈЩюШыЫМПМЃЉ
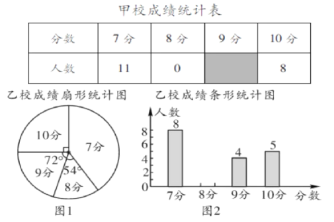
ЮвУЧжЊЕРЃЌгаРэЪ§ЕФМѕЗЈдЫЫуПЩвдзЊЛЏЮЊМгЗЈдЫЫуЃЌГ§ЗЈдЫЫуПЩвдзЊЛЏЮЊГЫЗЈдЫЫуЃЌгаРэЪ§ЕФГ§ЗНдЫЫуШчКЮзЊЛЏЮЊГЫЗНдЫЫуФиЃП
Ђё.ЪдвЛЪдЃЌЗТееЩЯУцЕФЫуЪНЃЌНЋЯТСадЫЫуНсЙћжБНгаДГЩУнЕФаЮЪН.- ![]() ________ЃЛ
________ЃЛ![]() ________.
________.
Ђђ.ЯывЛЯыЃКНЋвЛИіЗЧСугаРэЪ§ ![]() ЕФШІ /span>
ЕФШІ /span>![]() ДЮЗНаДГЩУнЕФаЮЪНЕШгк________.
ДЮЗНаДГЩУнЕФаЮЪНЕШгк________.
ЁОД№АИЁПЃЈ1ЃЉ![]() ЃЛ-8ЃЛCЃЈ2ЃЉ
ЃЛ-8ЃЛCЃЈ2ЃЉ![]() ЃЛ
ЃЛ![]() ЃЛ
ЃЛ![]()
ЁОНтЮіЁП
ЃЈ1ЃЉЂё. ИљОнГ§ЗНЕФЖЈвхМЦЫуЃЌАбСЌГ§ЛЏЮЊСЌГЫНјааМЦЫуМДПЩЃЛ
Ђђ.ИљОнГ§ЗНЕФЖЈвхМЦЫуШІ3ДЮЗНЃЌСНИіЛЅЮЊЕЙЪ§ЕФШІnДЮЗНЃЌБШНЯНсЙћМДПЩЃЛИКЪ§ЕФШІnДЮЗНЃЌЕБnЮЊЦцЪ§ЪБЃЌНсЙћЮЊИКЃЛЕБnЮЊХМЪ§ЪБЃЌНсЙћЮЊе§.
ЃЈ2ЃЉЗжБ№ИљОнГ§ЗНЕФдЫЫуЗЈдђМЦЫуМДПЩЃЌзюКѓЕУГіЙцТЩ![]() (nЁн3).
(nЁн3).
ЃЈ1ЃЉ Ђё.![]() =2ЁТ2ЁТ2=2ЁС
=2ЁТ2ЁТ2=2ЁС![]() ЁС
ЁС![]() =
=![]() ЃЌ
ЃЌ
![]() .
.
Ђђ. AЁЂЩшетИіЪ§ЮЊaЃЈaЁй0ЃЉЃЌдђ![]() е§ШЗЃЌВЛЗћКЯЬтвтЃЛ
е§ШЗЃЌВЛЗћКЯЬтвтЃЛ
BЁЂЩшетИіЪ§ЮЊaЃЈaЁй0ЃЉЃЌaЕФnДЮЗНЯдШЛЛЅЮЊЕЙЪ§ЃЌ ![]() ,
,![]() ПЩМћaЕФШІnДЮЗНвВЛЅЮЊЕЙЪ§ЃЌе§ШЗЃЌВЛЗћКЯЬтвтЃЛ
ПЩМћaЕФШІnДЮЗНвВЛЅЮЊЕЙЪ§ЃЌе§ШЗЃЌВЛЗћКЯЬтвтЃЛ
CЁЂ(-1)![]() =-1ЃЌ(-1)
=-1ЃЌ(-1)![]() =1ЃЌ ДэЮѓЃЌЗћКЯЬтвтЃЛ
=1ЃЌ ДэЮѓЃЌЗћКЯЬтвтЃЛ
DЁЂ ИКЪ§ЕФШІЦцЪ§ДЮЗНПЩвдЛЏЮЊЦцЪ§ИіИКЪ§ЯрГЫЃЌНсЙћЪЧИКЪ§ЃЌ ИКЪ§ЕФШІХМЪ§ДЮЗНПЩвдЛЏЮЊХМЪ§ИіИКЪ§ЯрГЫЃЌНсЙћЪЧе§Ъ§ЃЌе§ШЗЃЌВЛЗћКЯЬтвт.
ЙЪД№АИЮЊЃК ![]() ,-8, C.
,-8, C.
ЃЈ2ЃЉ -![]() -5ЁС
-5ЁС ![]() =-
=-![]() ЃЛ
ЃЛ
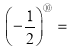 (-
(-![]() )ЁС
)ЁС ![]() =
=![]() =28ЃЛ
=28ЃЛ
Ђђ.![]() ЃЈnЁн3ЃЉ.
ЃЈnЁн3ЃЉ.
ЙЪД№АИЮЊЃК-![]() ЃЌ 28ЃЌ
ЃЌ 28ЃЌ ![]() .
.

 ЬьЬьЯђЩЯвЛБОКУОэЯЕСаД№АИ
ЬьЬьЯђЩЯвЛБОКУОэЯЕСаД№АИ аЁбЇЩњ10ЗжжггІгУЬтЯЕСаД№АИ
аЁбЇЩњ10ЗжжггІгУЬтЯЕСаД№АИ