Question

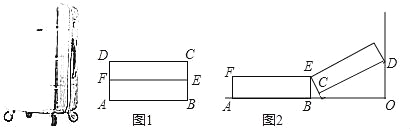
【题目】如图1所示旅行箱的箱盖和箱底两部分的厚度相同，图1中四边形ABCD形如矩形的旅行箱一侧的示意图，F为AD的中点，EF∥CD，现将放置在地面上的箱子打开，使箱盖的一端靠在墙上点D处，O为墙角，图2为箱子打开后的示意图，若箱子厚度AD=30cm，宽度AB=50cm．

（1）图2中，EC= cm，当点D与点O重合时，AO的长为 cm．

（2）若∠CDO=60°，求AO的长（结果取整数值）

（参考数据：sin60°=0.87，cos60°=0.5，tan60°=≈1.73，可使用科学计算器）

Answer 1

【答案】（1）15，100；（2）101cm．

【解析】

试题分析：（1）根据EC=BC=AD，AO=AB+CD=2AB即可解决问题；（2）过点C作OA的平行线，分别交BE和OD于H，G，根据∠CDO=60°，分别求出CG、HC，求出HG的长，就求出了BO的长，从而求出了AO的长.

试题解析：（1）∵EF∥AB∥CD，DF=AF，∴EC=EB=BC=AD=15cm，当点D与点O重合时，∵AB=B0=50，∴AO=50+50=100cm．故答案为15，100；（2）过点C作OA的平行线，如图：

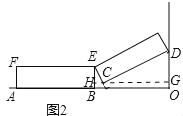分别交BE和OD于H，G．∵EB⊥OA，OD⊥OA，∴HG=HC+CG=OB，∵∠ECD=90°，∠CDO=60°，∴∠DCG=30°，∠ECH=60°，∵CD=50cm，EC=15cm，∴HC=EC=7.5cm，CG=CDsin60°=50×0.87≈43.5cm，∴AO=AB+OB=AB+HC+CG=50+7.5+43.5=101cm.