题目内容
现有直径为2的半圆O和一块等腰直角三角板
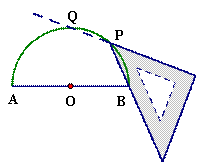
(1)将三角板如图1放置,锐角顶点P在圆上,斜边经过点B,一条直角边交圆于点Q,则BQ的长为
;
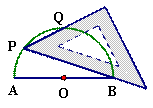
(2)将三角板如图2放置,锐角顶点P在圆上,斜边经过点B,一条直角边的延长线交圆于Q,则BQ的长为
.
(1)将三角板如图1放置,锐角顶点P在圆上,斜边经过点B,一条直角边交圆于点Q,则BQ的长为
| 2 |
| 2 |
(2)将三角板如图2放置,锐角顶点P在圆上,斜边经过点B,一条直角边的延长线交圆于Q,则BQ的长为
| 2 |
| 2 |

分析:(1)连接OQ、BQ,由于∠QPB=45°,根据圆周角定理得∠QOB=90°,则△QOB为等腰直角三角形,然后根据等腰直角三角形的性质可得BQ=
OB=
;
(2)连接AQ、OQ、BQ,由于∠QPB的外角为45°,根据圆内接四边形的性质得到∠A=45°,再根据圆周角定理得∠QOB=90°,则△QOB为等腰直角三角形,然后根据等腰直角三角形的性质可得BQ=
OB=
.
| 2 |
| 2 |
(2)连接AQ、OQ、BQ,由于∠QPB的外角为45°,根据圆内接四边形的性质得到∠A=45°,再根据圆周角定理得∠QOB=90°,则△QOB为等腰直角三角形,然后根据等腰直角三角形的性质可得BQ=
| 2 |
| 2 |
解答:解:(1)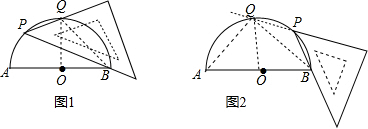 连接OQ、BQ,如图,
连接OQ、BQ,如图,
∵∠QPB=45°,
∴∠QOB=90°,
∴△QOB为等腰直角三角形,
而OB=1,
∴BQ=
OB=
;
(2)连接AQ、OQ、BQ,
∵∠QPB的外角为45°,
∴∠A=45°,
∴∠QOB=90°,
∴△QOB为等腰直角三角形,
而OB=1,
∴BQ=
OB=
.
故答案为
;
.
 连接OQ、BQ,如图,
连接OQ、BQ,如图,∵∠QPB=45°,
∴∠QOB=90°,
∴△QOB为等腰直角三角形,
而OB=1,
∴BQ=
| 2 |
| 2 |
(2)连接AQ、OQ、BQ,
∵∠QPB的外角为45°,
∴∠A=45°,
∴∠QOB=90°,
∴△QOB为等腰直角三角形,
而OB=1,
∴BQ=
| 2 |
| 2 |
故答案为
| 2 |
| 2 |
点评:本题考查了圆周角定理:在同圆或等圆中,相等的弧所对的圆周角相等,一条弧所对的圆周角的度数等于它所对的圆心角度数的一半.也考查了等腰直角三角形的判定与性质以及圆内接四边形的性质.

练习册系列答案
相关题目
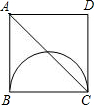 E沿线段BA以1cm/s的速度向点A运动,点F沿折线A-D-C以2cm/s的速度向点C运动,设点E离开点B的时间为t(秒).
E沿线段BA以1cm/s的速度向点A运动,点F沿折线A-D-C以2cm/s的速度向点C运动,设点E离开点B的时间为t(秒). 如图,正方形ABCD中,有一直径为BC的半圆,BC=2厘米,现有两点E、F,分别从点B,点A同时出发,点E沿线段BA以1厘米/秒的速度向点A运动,点F沿折线A-D-C以2厘米/秒的速度向C运动,设点E离开B的时间为t秒.
如图,正方形ABCD中,有一直径为BC的半圆,BC=2厘米,现有两点E、F,分别从点B,点A同时出发,点E沿线段BA以1厘米/秒的速度向点A运动,点F沿折线A-D-C以2厘米/秒的速度向C运动,设点E离开B的时间为t秒.