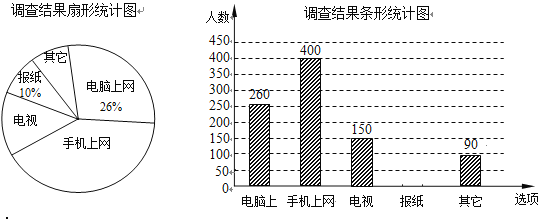
题目内容
【题目】如图,已知a∥b,长方形ABCD的点A在直线a上,B,C,D三点在平面上移动变化(长方形形状大小始终保持不变),请根据如下条件解答: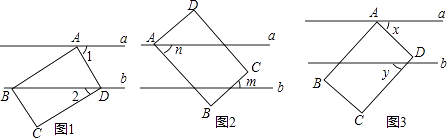
(1)图1,若点B、D在直线b上,点C在直线b的下方,∠2=30°,则∠1=;
(2)图2,若点D在直线a的上方,点C在平行直线a,b内,点B在直线b的下方,m,n表示角的度数,请写出m与n的数量关系并说明理由;
(3)图3,若点D在平行直线a,b内,点B,C在直线b的下方,x,y表示角的度数(x>y),且满足关系式x2﹣2xy+y2=100,求x的度数.
【答案】
(1)60°
(2)解:如图2,过C作EF∥a,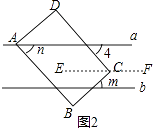
∵四边形ABCD是矩形,
∴AB∥CD,
∴n=∠4,
∵a∥b,EF∥a,
∴EF∥a∥b,
∴∠4=∠DCE ,∠ECB=m;
∴∠4+m=∠BCD=90°,
∴m+n=90°;
(3)解:如图3,过D作c∥b,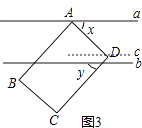
∵x2﹣2xy+y2=100,
∴(x﹣y)2=100,
∵x>y,
∴x﹣y=﹣10(舍去),
∴x﹣y=10,①
∵a∥b,c∥b,
∴a∥b∥c,
∵∠ADC=90°,
∴x+y=90,②
①+②得:x=50°.
【解析】(1)∵四边形ABCD是长方形,
∴∠ADC=90°,
∵∠2=30°,
∴∠ADB=60°,
∵a∥b,
∴∠1=∠ADB=60°,
故答案为:60°;
(1)根据矩形的四个角都是直角得出∠ADC=90°,根据角的和差得出∠ADB=60°,根据二直线平行内错角相等得出∠1=∠ADB=60°;
(2)过C作EF∥a,根据矩形的对边互相平行得出AB∥CD,根据二直线平行同位角相等得出n=∠4,根据平行于同一直线的两条直线互相平行得出EF∥a∥b,根据二直线平行,内错角相等得出∠4=∠DCE ,∠ECB=m;根据等式的性质得出结论;
(3)将方程x2﹣2xy+y2=100,利用直接开平方法得出x﹣y=10,①,根据平行于同一直线的两条直线互相平行得出a∥b∥c,根据二直线平行,内错角相等,及等式的性质得出结论。

 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案 初中学业考试导与练系列答案
初中学业考试导与练系列答案