题目内容
如图,若点A在数轴上对应的数为a,点B在数轴上对应的数为b,且a,b满足|a+2|+(b-1)2=0.

(1)求线段AB的长;
(2)点C在数轴上对应的数为x,且x是方程2x-1=
x+2的解,在数轴上是否存在点P,使PA+PB=PC,若存在,直接写出点P对应的数;若不存在,说明理由;
(3)在(1)的条件下,将点B向右平移5个单位长度至点B’,此时在原点O处放一挡板,一小球甲从点A处以1个单位长度/秒的速度向左运动;同时另一小球乙从点B’处以2个单位长度/秒的速度也向左运动,在碰到挡板后(忽略球的大小,可看作一点)以原来的速度向相反的方向运动,设运动的时间为t(秒),求甲、乙两小球到原点的距离相等时经历的时间.

(1)求线段AB的长;
(2)点C在数轴上对应的数为x,且x是方程2x-1=
| 1 | 2 |
(3)在(1)的条件下,将点B向右平移5个单位长度至点B’,此时在原点O处放一挡板,一小球甲从点A处以1个单位长度/秒的速度向左运动;同时另一小球乙从点B’处以2个单位长度/秒的速度也向左运动,在碰到挡板后(忽略球的大小,可看作一点)以原来的速度向相反的方向运动,设运动的时间为t(秒),求甲、乙两小球到原点的距离相等时经历的时间.
分析:(1)根据绝对值及完全平方的非负性,可得出a、b的值,继而可得出线段AB的长;
(2)先求出x的值,再由PA+PB=PC,可得出点P对应的数.
(3)
(2)先求出x的值,再由PA+PB=PC,可得出点P对应的数.
(3)
解答:解(1)∵|a+2|+(b-1)2=0,
∴a=-2,b=1,
∴AB=b-a=1-(-2)=3.
(2)2x-1=
x+2,
解得:x=2,
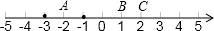
由题意得,点P只能在点B的左边,
①当点P在AB之间时,x+2+1-x=2-x,
解得:x=-1;
②当点P在A点左边时,-2-x+1-x=2-x,
解得:x=-3,
综上可得P所对应的数是-3或-1.
(3)①甲、乙两球均向左运动,即0≤t≤3时,
此时OA=2+t,OB’=6-2t,
则可得方程2+t=6-2t,
解得t=
;
②甲继续向左运动,乙向右运动,即t>3时,
此时OA=2+t,OB’=2t-6,
则可得方程2+t=2t-6,
解得t=8.
答:甲、乙两小球到原点的距离相等时经历的时间为
秒或8秒.
∴a=-2,b=1,
∴AB=b-a=1-(-2)=3.
(2)2x-1=
| 1 |
| 2 |
解得:x=2,
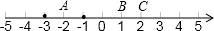
由题意得,点P只能在点B的左边,
①当点P在AB之间时,x+2+1-x=2-x,
解得:x=-1;
②当点P在A点左边时,-2-x+1-x=2-x,
解得:x=-3,
综上可得P所对应的数是-3或-1.
(3)①甲、乙两球均向左运动,即0≤t≤3时,
此时OA=2+t,OB’=6-2t,
则可得方程2+t=6-2t,
解得t=
| 4 |
| 3 |
②甲继续向左运动,乙向右运动,即t>3时,
此时OA=2+t,OB’=2t-6,
则可得方程2+t=2t-6,
解得t=8.
答:甲、乙两小球到原点的距离相等时经历的时间为
| 4 |
| 3 |
点评:本题考查了一元一次方程的应用及数轴的知识,注意在求解未知数的时候,我们可以设出这个量,然后根据题目的等量关系列方程求解.

练习册系列答案
相关题目

 已知点A、B在数轴上的位置如图.
已知点A、B在数轴上的位置如图.
 x+2的解,在数轴上是否存在点P,使PA+PB=PC,若存在,直接写出点P对应的数;若不存在,说明理由;
x+2的解,在数轴上是否存在点P,使PA+PB=PC,若存在,直接写出点P对应的数;若不存在,说明理由;