题目内容
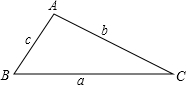
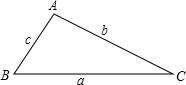
设△ABC的三边依次为a,b,c,且满足a3+b3+a2b+ab2-ac2-bc2=0,则△ABC的形状是
- A.直角三角形
- B.等边三角形
- C.等腰三角形
- D.等腰直角三角形
A
因为a3+b3+a2b+ab2-ac2-bc2=0,所以(a+b)(a2+b2-c2)=0,又因为a+b≠0,所以a2+b2-c2=0,即a2+b2=c2,所以△ABC是直角三角形.
因为a3+b3+a2b+ab2-ac2-bc2=0,所以(a+b)(a2+b2-c2)=0,又因为a+b≠0,所以a2+b2-c2=0,即a2+b2=c2,所以△ABC是直角三角形.

练习册系列答案
相关题目
 (a+b+c)
(a+b+c)