题目内容
若n是正整数,下列代数式中,哪一个代数式的值一定不是某个自然数的平方( )
分析:分别将各选项提取公因式,然后运用特殊值判断法判断两因式是相乘后是否可以为一个数的平方,从而可得出答案.
解答:解:A、3n2-3n+3=3(n2-n+1),则当n2-n+1=3时,即n=2时可使3n2-3n+3为3的平方,故本选项错误.
B、4n2+4n+4=22(n2+n+1),则只有n2+n+1是完全平方式时才能满足4n2+4n+4是一个数的平方,而n2+n+1不是完全平方式,故本选项正确;
C、5n2-5n-5=5(n2-n-1),则当n2-n-1=5时,即n=3时可使5n2-5n-5为5的平方,故本选项错误;
D、7n2-7n+7=7(n2-n+1),则当n2-n+1=7时,即n=3时可使7n2-7n+7为7的平方,故本选项错误.
综上可得选项B正确.
故选B.
B、4n2+4n+4=22(n2+n+1),则只有n2+n+1是完全平方式时才能满足4n2+4n+4是一个数的平方,而n2+n+1不是完全平方式,故本选项正确;
C、5n2-5n-5=5(n2-n-1),则当n2-n-1=5时,即n=3时可使5n2-5n-5为5的平方,故本选项错误;
D、7n2-7n+7=7(n2-n+1),则当n2-n+1=7时,即n=3时可使7n2-7n+7为7的平方,故本选项错误.
综上可得选项B正确.
故选B.
点评:此题考查了完全平方数的知识,有一定的难度,如果一个整式提取的公因数是完全平方数,则要使这个因式可以为一个数的平方,则这个剩余的因式一定是完全平方式.

练习册系列答案
相关题目
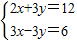 的求解方法是消元法,即可将它化为一元一次方程来解,可求得方程组
的求解方法是消元法,即可将它化为一元一次方程来解,可求得方程组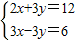 有唯一解.
有唯一解.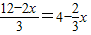
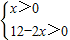 则有0<x<6
则有0<x<6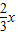 为正整数,则
为正整数,则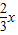 为正整数,所以x为3的倍数
为正整数,所以x为3的倍数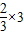 =2
=2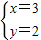
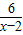 为正整数,则满足条件的x的值有几个.( )
为正整数,则满足条件的x的值有几个.( ) 的正整数解.
的正整数解.