题目内容
甲、乙两人同时同地出发相背而行,1小时后分别到达各自的目的地A、B,若仍以原来的速度出发并互换彼此到达的目的地,则甲在乙到达A地35分钟后到达B地,则甲乙两人的速度之比是
- A.
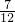
- B.

- C.

- D.
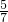
C
分析:设甲,乙的速度为未知数,那么可得到达目的地的路程.根据甲用的时间-乙用的时间=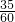 ,得到相应方程,整理即可.
,得到相应方程,整理即可.
解答:设甲,乙的速度为x千米/时,y千米/时,则甲的行程为x千米,乙的行程为y千米.
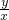 -
-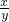 =
=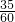 ,
,
设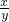 =a,则原方程变为
=a,则原方程变为 -a=
-a=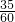 ,
,
a2+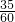 a-1=0,
a-1=0,
(a+ )(a-
)(a- )=0,
)=0,
解得a=- (不合题意,舍去);或a=
(不合题意,舍去);或a= ,
,
即甲乙两人的速度之比为 .
.
故选C.
点评:本题综合考查了一元二次方程及方式方程的应用;得到甲乙两人交换目的地所用的时间的等量关系是解决本题的关键;利用换元法求得甲乙两人的速度之比是解决本题的难点.
分析:设甲,乙的速度为未知数,那么可得到达目的地的路程.根据甲用的时间-乙用的时间=
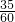 ,得到相应方程,整理即可.
,得到相应方程,整理即可.解答:设甲,乙的速度为x千米/时,y千米/时,则甲的行程为x千米,乙的行程为y千米.
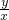 -
-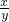 =
=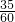 ,
,设
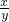 =a,则原方程变为
=a,则原方程变为 -a=
-a=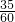 ,
,a2+
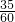 a-1=0,
a-1=0,(a+
 )(a-
)(a- )=0,
)=0,解得a=-
 (不合题意,舍去);或a=
(不合题意,舍去);或a= ,
,即甲乙两人的速度之比为
 .
.故选C.
点评:本题综合考查了一元二次方程及方式方程的应用;得到甲乙两人交换目的地所用的时间的等量关系是解决本题的关键;利用换元法求得甲乙两人的速度之比是解决本题的难点.

练习册系列答案
 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案
相关题目

