题目内容
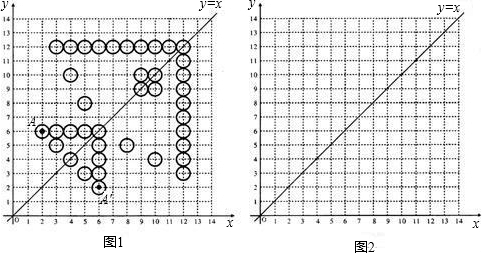
22、用围棋棋子可以在棋盘中摆出许多有趣的图案．如图1，在棋盘上建立平面直角坐标系，以直线y=x为对称轴，我们可以摆出一个轴对称图案（其中A与A′是对称点），你看它象不象一只美丽的鱼．
（1）请你在图2中，也用10枚以上的棋子摆出一个以直线y=x为对称轴的轴对称图案，并在所作的图形中找出两组对称点，分别标为B-B′，C-C′（注意棋子要摆在格点上）；
（2）在给定的平面直角坐标系中，你标出的B-B′、C-C′的坐标分别是：B（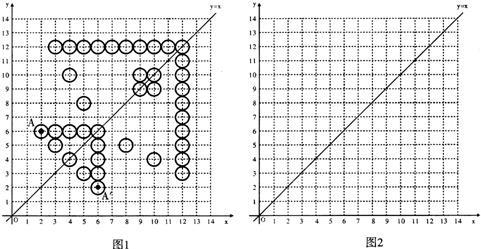
（1）请你在图2中，也用10枚以上的棋子摆出一个以直线y=x为对称轴的轴对称图案，并在所作的图形中找出两组对称点，分别标为B-B′，C-C′（注意棋子要摆在格点上）；
（2）在给定的平面直角坐标系中，你标出的B-B′、C-C′的坐标分别是：B（
0，6
），B′（6，0
），C（4，8
），C′（8，4
）；根据以上对称点坐标的规律，写出点P（a，b）关于对称轴y=x的对称点P′的坐标是（b，a
）．分析：（1）关于某条直线对称，对应点到这条直线的距离应相等．
（2）根据所标的对应点写出相应坐标，进而得到一般规律．
（2）根据所标的对应点写出相应坐标，进而得到一般规律．
解答：
解：（1）符合轴对称图形的要求即可（5分）．
（其中作图（4分），正确标出两组对称点得1分）
（2）（0，6）（6，0），（4，8），（8，4）．（4分）
P′9（b，a）得（1分）．
（本题满分10分）
解：（1）符合轴对称图形的要求即可（5分）．（其中作图（4分），正确标出两组对称点得1分）
（2）（0，6）（6，0），（4，8），（8，4）．（4分）
P′9（b，a）得（1分）．
（本题满分10分）
点评：本题构思新颖，富有创意，是一道考查图形变换、点的坐标、及探究图形变换与坐标关系的考题．一方面，它利用学生熟悉的围棋棋子来摆一个轴对称图形，这种趣味性的活动设计，不仅有效地考查了学生对轴对称的理解水平，又达到发展空间观念与几何直觉的目的；另一方面，结果的开放性以及范例所给美丽图案的暗示作用，令每-层次的学生都能轻易入手，又给部分学生施展才华的空间，使人人都能从中获得成功的体验．本例第2小题把试题推上了一个新的高度，它通过引导学生观察对称点的坐标特征，从而发现平面内关于y=x对称的两个点之间的坐标规律，不仅挖掘了轴对称的本质，更巧妙地把“数”与“形”有机地结合起来．本例的设计，体现《课程标准》所倡导的“动手实践、自主探索”的学习理念与让“不同的人在数学上得到不同的发展”的评价理念．
练习册系列答案
相关题目
